engineering core courses

Solid Mechanics I
 Course homepage
Solid Mechanics I
 Course homepage
C9: Deflections of Beams and Shafts
9.1 Integration Method
- Theory - Example - Question 1 - Question 2
9.2 Discontinuity Functions (Macaulay’s Method)
- Theory - Example - Question 1 - Question 2 - Question 3

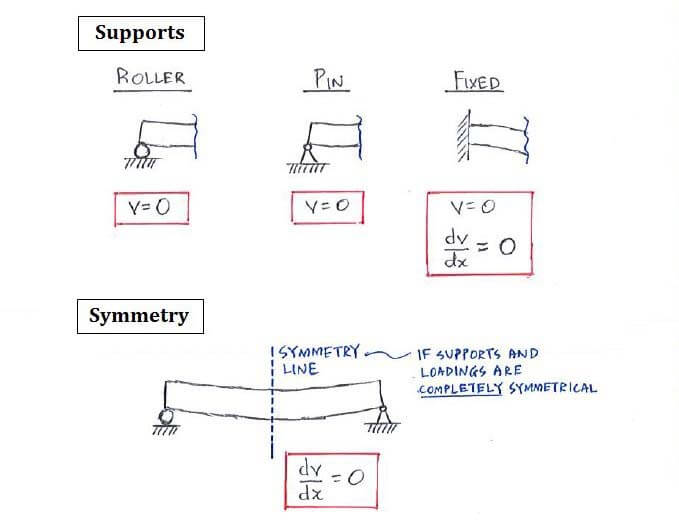
C9.1 Integration Method

The integration method allows us to obtain the slope and deflection at a particular point on the beam. These information are crucial to the design of beams and shafts to ensure they meet the safe design criteria.

To get our slope and deflection, we start with this relation:


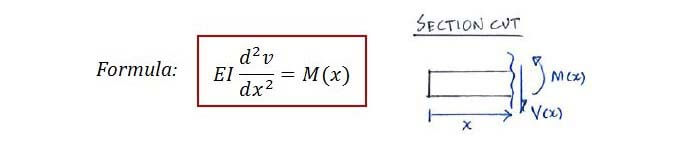
Moment relation for double integration method
Note:
  • EI is called the flexural rigidity. It is the Young’s modulus E multiplied by the moment of inertia I.
  • ν is the deflection (units: m or mm)
  • M(x) is the internal bending moment, expressed as a function of x, which is the distance along the beam.

C9.1 Integration Method

The integration method allows us to obtain the slope and deflection at a particular point on the beam. These information are crucial to the design of beams and shafts to ensure they meet the safe design criteria.

To get our slope and deflection, we start with this relation:


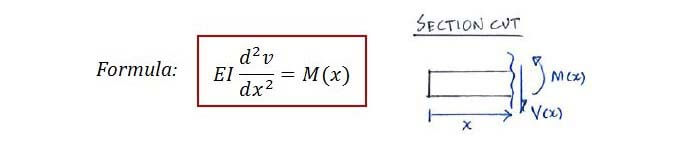
Moment relation for double integration method
Note:
  • EI is called the flexural rigidity. It is the Young’s modulus E multiplied by the moment of inertia I.
  • ν is the deflection (units: m or mm)
  • M(x) is the internal bending moment, expressed as a function of x, which is the distance along the beam.

Then, using the relation above, you integrate once to get dν/dx (slope) and another time to get ν (deflection):


Integrating moment equation twice to get deflection equation a.k.a elastic curve

You can then shift the EI term over the right-hand-side to get your slope (dν/dx) or deflection (ν).

Notice that integrating twice produced two constants C1 and C2. How do we resolve these? That’s where our boundary conditions (BCs) come in =)

Boundary conditions (BCs)

Boundary conditions are usually taken at the supports. If the beam is symmetrical, BCs can be taken at the point of symmetry as well:


Boundary conditions to get constants from double integration method

There are 2 constants C1 and C2, and therefore we need to apply 2 BCs to solve for both C1 and C2.

The integration method might seem long and complex, but don’t worry, it’s easier than it looks. The best way to learn is by example.

Then, using the relation above, you integrate once to get dν/dx (slope) and another time to get ν (deflection):


Integrating moment equation twice to get deflection equation a.k.a elastic curve

You can then shift the EI term over the right-hand-side to get your slope (dν/dx) or deflection (ν).

Notice that integrating twice produced two constants C1 and C2. How do we resolve these? That’s where our boundary conditions (BCs) come in =)

Boundary conditions (BCs)

Boundary conditions are usually taken at the supports. If the beam is symmetrical, BCs can be taken at the point of symmetry as well:


Boundary conditions to get constants from double integration method

There are 2 constants C1 and C2, and therefore we need to apply 2 BCs to solve for both C1 and C2.

The integration method might seem long and complex, but don’t worry, it’s easier than it looks. The best way to learn is by example.

engineering core courses

COURSES FEATURES THE STORY CONTACT US ECC facebook link
engineering core courses