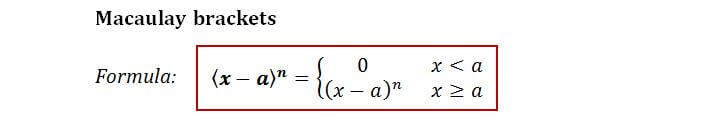C9.2 Discontinuity Functions (Macaulay’s Method)
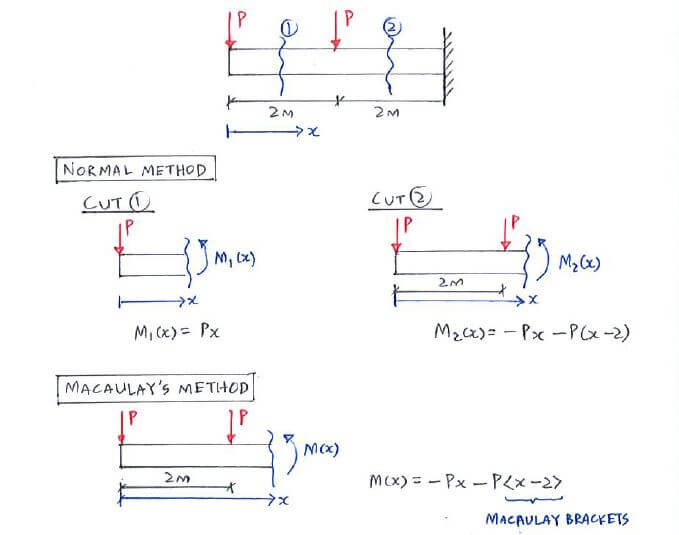
We saw in Question 2 of Chapter 9.1 that when a new load is introduced along the beam, the moment equation changes and we need a separate elastic curve equation to fully define the beam.
That’s pretty tedious ain’t it? Fortunately, we have what we call discontinuity functions that allow us to have an elastic curve that fully defines the beam, regardless of the number of loadings. How does this work?
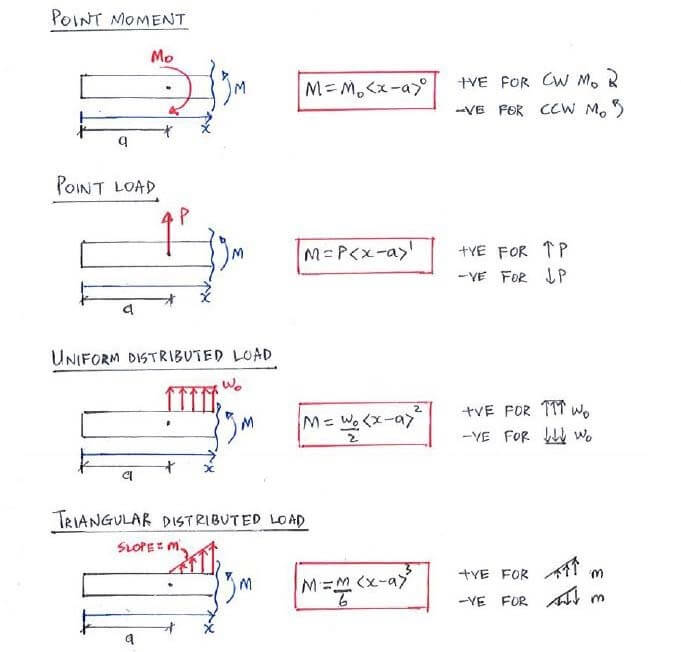
We use what we call “Macaulay brackets”, that will only be “activated” when our distance x moves past where the load is applied:
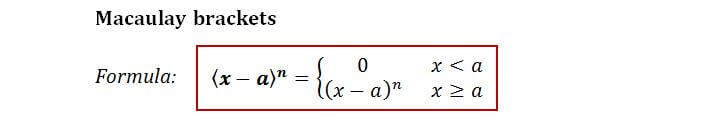
C9.2 Discontinuity Functions (Macaulay’s Method)
We saw in Question 2 of Chapter 9.1 that when a new load is introduced along the beam, the moment equation changes and we need a separate elastic curve equation to fully define the beam.
That’s pretty tedious ain’t it? Fortunately, we have what we call discontinuity functions that allow us to have an elastic curve that fully defines the beam, regardless of the number of loadings. How does this work?
We use what we call “Macaulay brackets”, that will only be “activated” when our distance x moves past where the load is applied: