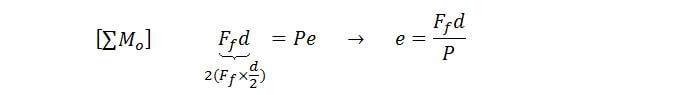In all our previous examples, we’ve looked only at cross-sections that are symmetrical. But what happens when we have a shear force acting through a centroid of a non-symmetrical cross-section? Here’s what happens:
In all our previous examples, we’ve looked only at cross-sections that are symmetrical. But what happens when we have a shear force acting through a centroid of a non-symmetrical cross-section? Here’s what happens:
It twists! The reason for this is because of the internal shear flow which causes a net torque on the cross-section:
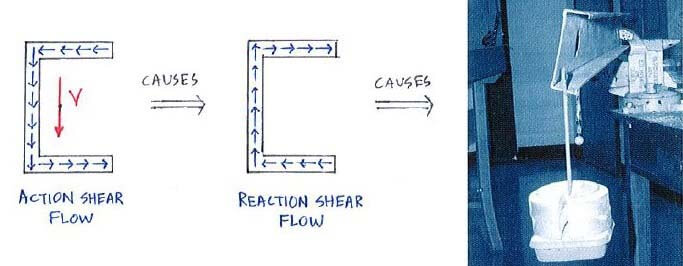
Note that we usually look at shear flow in terms of the action shear flow (same direction as V), but it is the reaction shear flow (opposite direction) that causes the twisting. For consistency, we will present the following shear flow in the action shear flow direction.
Fortunately there is a way to overcome this. We can apply the shear force at an offset, such that the torque caused by the shear force balanced the torque caused by the reaction shear flow. The position of this offset is what we call our shear centre.
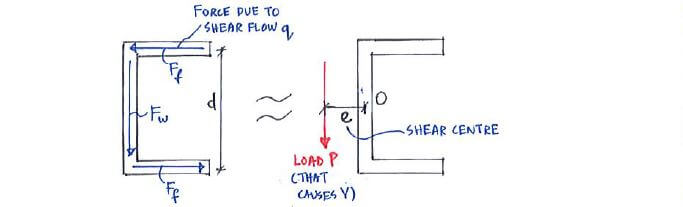
To calculate the position of our shear centre e, all we do is take the sum of moments about O for the forces acting due to q, and equate that to the moment caused by P acting at e:
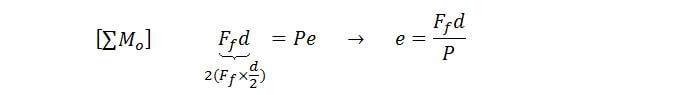
For other types of cross-section, the same principle applies: taking sum of moments due to other shear flow forces and use that to find the shear centre e.
Let’s look at an example now.
It twists! The reason for this is because of the internal shear flow which causes a net torque on the cross-section:
Note that we usually look at shear flow in terms of the action shear flow (same direction as V), but it is the reaction shear flow (opposite direction) that causes the twisting. For consistency, we will present the following shear flow in the action shear flow direction.
Fortunately there is a way to overcome this. We can apply the shear force at an offset, such that the torque caused by the shear force balanced the torque caused by the reaction shear flow. The position of this offset is what we call our shear centre.
To calculate the position of our shear centre e, all we do is take the sum of moments about O for the forces acting due to q, and equate that to the moment caused by P acting at e:
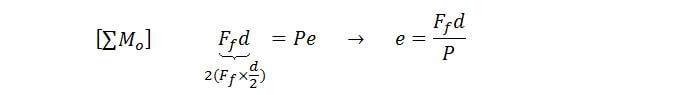
For other types of cross-section, the same principle applies: taking sum of moments due to other shear flow forces and use that to find the shear centre e.
Let’s look at an example now.