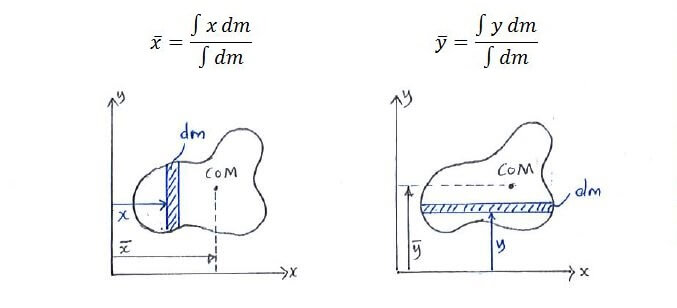
C4.1 Centre of Mass
We’ve been looking at weights as point loads. But mass/objects in reality occupy a volume, and therefore the weight is acting in a distributive manner rather than as a point load.
However we can still treat it as a point load if we find a point in the mass which represents the effective single point where the total weight is acting on. This is called the centre of mass (CoM).
It is useful to find the CoM as it helps us to simplify our statics calculations:
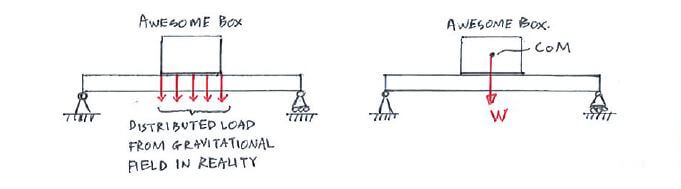
C4.1 Centre of Mass
We’ve been looking at weights as point loads. But mass/objects in reality occupy a volume, and therefore the weight is acting in a distributive manner rather than as a point load.
However we can still treat it as a point load if we find a point in the mass which represents the effective single point where the total weight is acting on. This is called the centre of mass (CoM).
It is useful to find the CoM as it helps us to simplify our statics calculations: