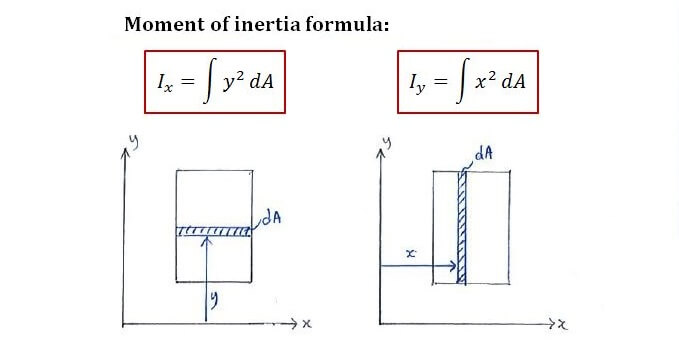
Note that the units for MoI is m4 (y2 [m2] × dA [m2] = m4). Sometimes it might be more convenient to express the units as mm4.
When calculating MoI, setting the reference axis correctly is of utmost importance. The reference axis is where you take your y or x variables from (in the Ix = ∫y2 dA and Iy = ∫x2 dA formulas).
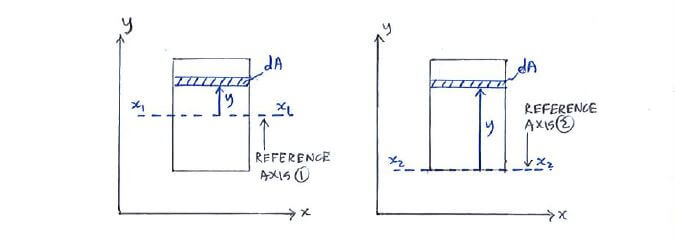
Calculating your MoI from either the x1-x1 or x2-x2 references axes will give you different values of MoI. You need to be certain of the reference axis that the question is asking you to calculate your MoI from.
Let’s look at an example now to illustrate this. Again, the examples are designed to show you the derivation of the moment of inertia formula for some of the common shapes. However in practical situations, you can usually referring to the table of moment of inertia formulas instead.

Note that the units for MoI is m4 (y2 [m2] × dA [m2] = m4). Sometimes it might be more convenient to express the units as mm4.
When calculating MoI, setting the reference axis correctly is of utmost importance. The reference axis is where you take your y or x variables from (in the Ix = ∫y2 dA and Iy = ∫x2 dA formulas).

Calculating your MoI from either the x1-x1 or x2-x2 references axes will give you different values of MoI. You need to be certain of the reference axis that the question is asking you to calculate your MoI from.
Let’s look at an example now to illustrate this. Again, the examples are designed to show you the derivation of the moment of inertia formula for some of the common shapes. However in practical situations, you can usually referring to the table of moment of inertia formulas instead.