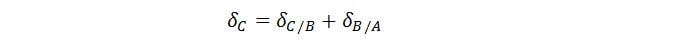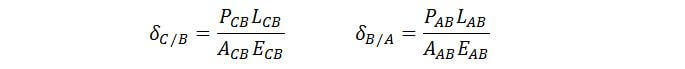C2.2 Statically Indeterminate Analysis

What happens when we don’t have enough equations to solve for all unknown reaction supports? Consider the following bar with 2 fixed ends:

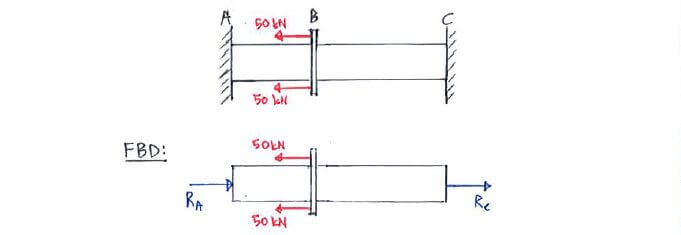
Statically Indeterminate scenario

We have 2 unknowns (R_A and R_C) but only one equation (ΣF_x = 0). How do we solve this then? Well we can actually get the 2nd equation by considering the deflection at the ends of the bar. The forces of different magnitudes cause varying displacements along the bar, but we know that the deflections at both ends are zero, since they are fixed. Therefore:

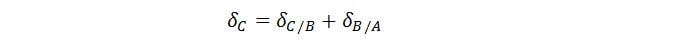
Statically Indeterminate deformation

C2.2 Statically Indeterminate Analysis

What happens when we don’t have enough equations to solve for all unknown reaction supports? Consider the following bar with 2 fixed ends:

Statically Indeterminate scenario

We have 2 unknowns (R_A and R_C) but only one equation (ΣF_x = 0). How do we solve this then? Well we can actually get the 2nd equation by considering the deflection at the ends of the bar. The forces of different magnitudes cause varying displacements along the bar, but we know that the deflections at both ends are zero, since they are fixed. Therefore:

Statically Indeterminate deformation

Using the elastic deformation formula, we can then express the displacements in terms of the forces:

Elastic deformation for statically indeterminate scenario

P_CB and P_AB can be expressed as the reaction forces, and this gives us our 2nd equation to solve for the 2 unknown reactions. The displacement equation is called the compatibility equation.

Let’s look at an example now.

Using the elastic deformation formula, we can then express the displacements in terms of the forces:

Elastic deformation for statically indeterminate scenario

P_CB and P_AB can be expressed as the reaction forces, and this gives us our 2nd equation to solve for the 2 unknown reactions. The displacement equation is called the compatibility equation.

Let’s look at an example now.