engineering core courses

Solid Mechanics I
 Course homepage
Solid Mechanics I
 Course homepage
C4: Bending
4.1 Shear Force and Bending Moment Diagrams
- Theory - Example
4.2 Flexure Formula
- Theory - Example - Question 1 - Question 2 - Question 3

C4.1 Shear Force and Bending Moment Diagrams

In this chapter, we seek to calculate the stress from bending which is caused by bending moments. As such, constructing the SF and BM diagrams is necessary to obtain the BM magnitude along the beam, so that we can calculate the resulting bending stress.

SF and BM diagrams were originally covered in Chapter 5.3 of Statics, so we will only give you a brief summary on how to construct SFBM diagrams here. You can refer to the original Chapter 5.3 for the full explanation.

Basically, there are two methods to construct SF and BM diagrams:

  1. Method 1: Equation approach − SFBM diagrams are constructed by considering the equation of SF and BM. Not recommended, but if you are keen on brushing up your memory, you can refer here for the explanation of the method.
  2. Method 2: Direct method − This is the method we will be using most in this chapter, and we'll explain more about this method below.

C4.1 Shear Force and Bending Moment Diagrams

In this chapter, we seek to calculate the stress from bending which is caused by bending moments. As such, constructing the SF and BM diagrams is necessary to obtain the BM magnitude along the beam, so that we can calculate the resulting bending stress.

SF and BM diagrams were originally covered in Chapter 5.3 of Statics, so we will only give you a brief summary on how to construct SFBM diagrams here. You can refer to the original Chapter 5.3 for the full explanation.

Basically, there are two methods to construct SF and BM diagrams:

  1. Method 1: Equation approach − SFBM diagrams are constructed by considering the equation of SF and BM. Not recommended, but if you are keen on brushing up your memory, you can refer here for the explanation of the method.
  2. Method 2: Direct method − This is the method we will be using most in this chapter, and we'll explain more about this method below.

Direct method for constructing SFBM diagrams

Basically this method works by directly constructing the SF diagram using the FBD, and BM diagram using both the SF diagram and FBD.

Two key relationships for this method are as follows:

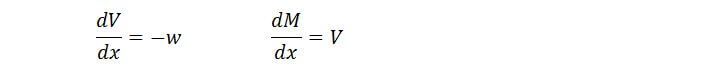
Gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V

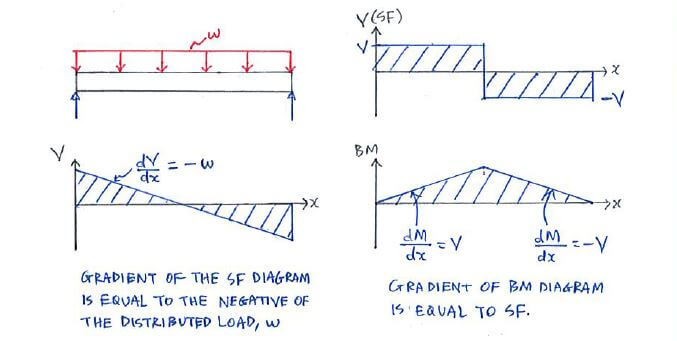
The relationships basically say that the gradient of the SF diagram is equal to the –ve of the distributed load, while the gradient of the BM diagram is equal to the SF:

Visualisation of gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V, in graph form

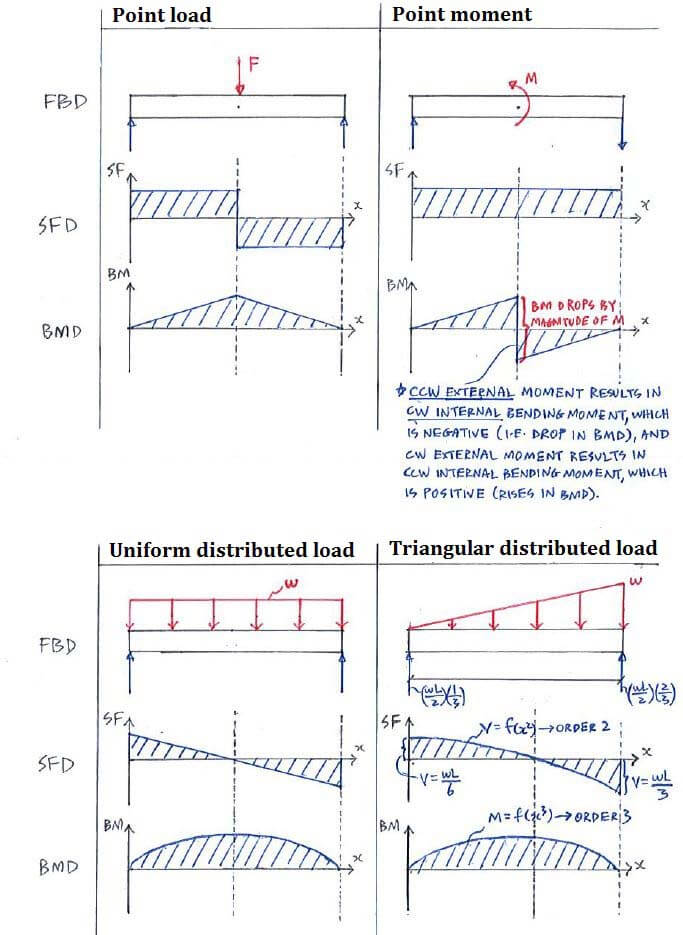
We also present to you a few examples of how different forces acting on a beam are represented in SF and BM diagrams:

Shear force and bending moment diagrams for common loads

If this all seem a little confusing to you, don't worry as we will be working through an example soon. But first, let's brush up our memory on sign conventions.

Sign convention

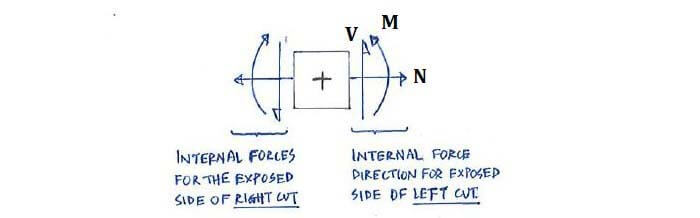
We touched on sign conventions for SFBM diagrams before in Chapter 5.2 of Statics. The positive directions for the normal force N, shear force V and bending moment M are shown below:

Sign convention for shear force and bending moment diagrams

Let’s look at an example now to brush up your memory. If you need more questions to practice, there are more questions here.

Direct method for constructing SFBM diagrams

Basically this method works by directly constructing the SF diagram using the FBD, and BM diagram using both the SF diagram and FBD.

Two key relationships for this method are as follows:

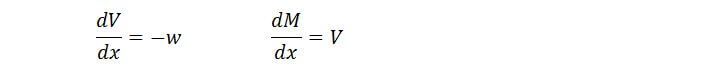
Gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V

The relationships basically say that the gradient of the SF diagram is equal to the –ve of the distributed load, while the gradient of the BM diagram is equal to the SF:

Visualisation of gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V, in graph form

We also present to you a few examples of how different forces acting on a beam are represented in SF and BM diagrams:

Shear force and bending moment diagrams for common loads

If this all seem a little confusing to you, don't worry as we will be working through an example soon. But first, let's brush up our memory on sign conventions.

Sign convention

We touched on sign conventions for SFBM diagrams before in Chapter 5.2 of Statics. The positive directions for the normal force N, shear force V and bending moment M are shown below:

Sign convention for shear force and bending moment diagrams

Let’s look at an example now to brush up your memory. If you need more questions to practice, there are more questions here.

engineering core courses

COURSES FEATURES THE STORY CONTACT US ECC facebook link
engineering core courses