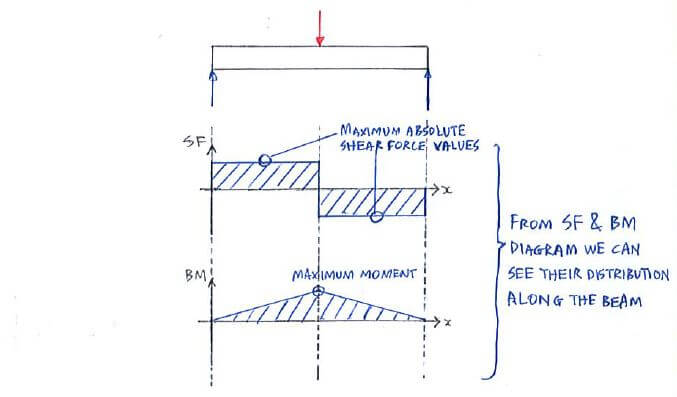
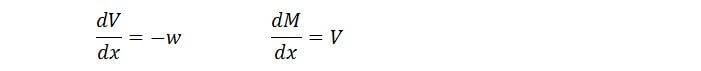C5.3 Shear Force and Bending Moment Diagrams

You probably can tell from the examples previously that the shear force SF and bending moment BM varies along the beam, due to the varying loads.

From an engineer’s point of view, you would want to find out where the maximum SF or BM is – i.e. the weakest part of the beam. This is so that you can design to ensure that it’s safe!

Likewise you would want to know where the minimum SF or BM is, so that you will not overdesign that portion of the beam.

So how do we conveniently see the SF and BM along the beam? Well that’s what the SF and BM diagrams are for!

Example of a shear force and bending moment (SFBM) diagram to view the SFBM distribution along a beam

C5.3 Shear Force and Bending Moment Diagrams

You probably can tell from the examples previously that the shear force SF and bending moment BM varies along the beam, due to the varying loads.

From an engineer’s point of view, you would want to find out where the maximum SF or BM is – i.e. the weakest part of the beam. This is so that you can design to ensure that it’s safe!

Likewise you would want to know where the minimum SF or BM is, so that you will not overdesign that portion of the beam.

So how do we conveniently see the SF and BM along the beam? Well that’s what the SF and BM diagrams are for!

Example of a shear force and bending moment (SFBM) diagram to view the SFBM distribution along a beam

There are 2 methods to construct the SF and BM diagrams:

Method 1: Equation approach

In this method, you basically obtain the expression for SF (or V) and BM (or M) as a function of the distance x from the left end of the beam. The equations are obtained using the equations of equilibrium such that the internal forces ensure equilibrium of the section cut:

Obtain equations for bending moment M and shear force V such that they maintain equilibrium of section cut

The equations obtained are then used to construct the SF and BM diagrams. Note that you will need one equation for every single change in loading (i.e. when a new force comes in, as you move from the left to right of the beam):

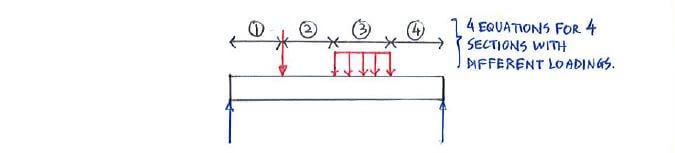
New equation for bending moment M and shear force V required when a new force gets introduced as you move from left to right of beam

It might seem vague at the moment, but it will make more sense once you work through an example.

Method 2: Direct method

This is the recommended method but it really takes practice to master. Basically this method works by directly constructing the SF diagram using the FBD, and BM diagram using both the SF diagram and FBD.

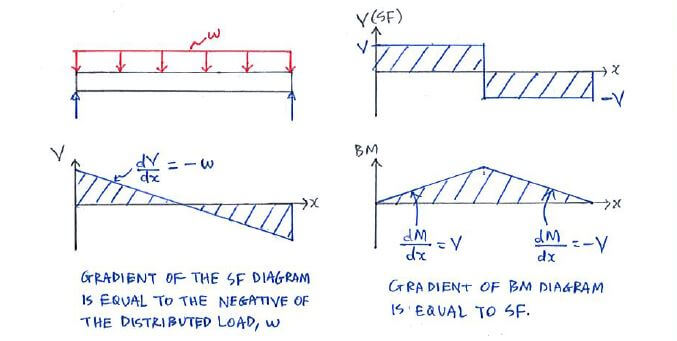
Two key relationships for this method are as follows:

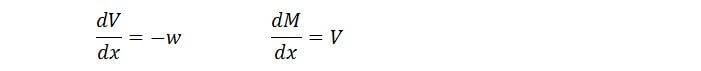
Gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V

The relationships basically say that the gradient of the SF diagram is equal to the –ve of the distributed load, while the gradient of the BM diagram is equal to the SF:

Visualisation of gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V, in graph form

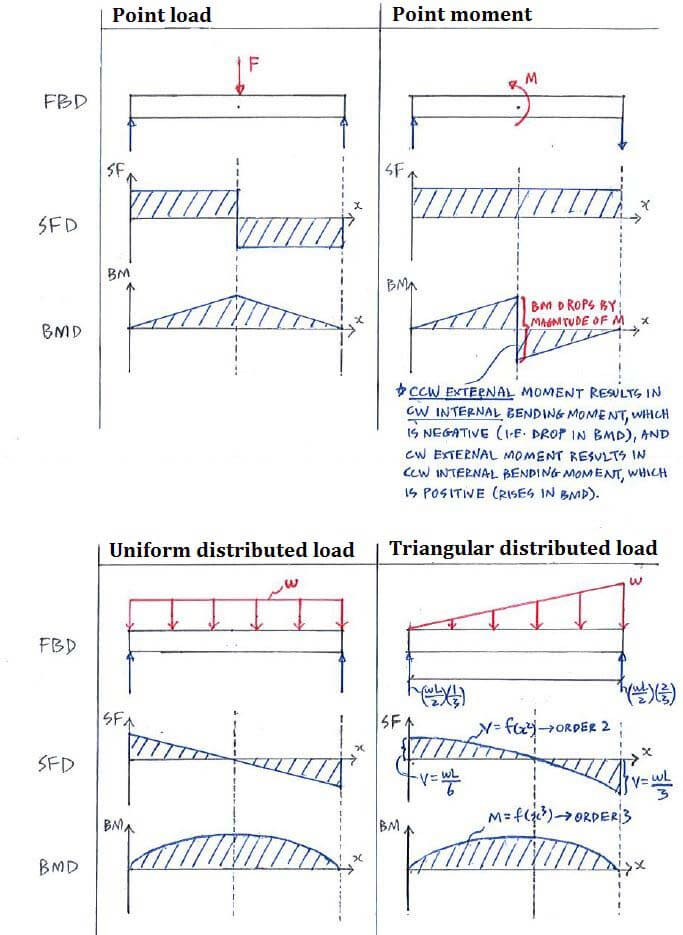
We also present to you a few examples of how different forces acting on a beam are represented in SF and BM diagrams:

Shear force and bending moment diagrams for common loads

So how do we actually construct the SF and BM diagrams directly? The best way to explain is through an example.

*By the way, SF and BM diagram is probably the most important topic in this entire Statics course. You will be using a lot of it even in future courses (Solid Mechanics I and Solid Mechanics II), so learn it well!

There are 2 methods to construct the SF and BM diagrams:

Method 1: Equation approach

In this method, you basically obtain the expression for SF (or V) and BM (or M) as a function of the distance x from the left end of the beam. The equations are obtained using the equations of equilibrium such that the internal forces ensure equilibrium of the section cut:

Obtain equations for bending moment M and shear force V such that they maintain equilibrium of section cut

The equations obtained are then used to construct the SF and BM diagrams. Note that you will need one equation for every single change in loading (i.e. when a new force comes in, as you move from the left to right of the beam):

New equation for bending moment M and shear force V required when a new force gets introduced as you move from left to right of beam

It might seem vague at the moment, but it will make more sense once you work through an example.

Method 2: Direct method

This is the recommended method but it really takes practice to master. Basically this method works by directly constructing the SF diagram using the FBD, and BM diagram using both the SF diagram and FBD.

Two key relationships for this method are as follows:

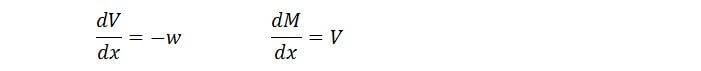
Gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V

The relationships basically say that the gradient of the SF diagram is equal to the –ve of the distributed load, while the gradient of the BM diagram is equal to the SF:

Visualisation of gradient of shear force V equals -ve of distributed load w; gradient of bending moment BM equals shear force V, in graph form

We also present to you a few examples of how different forces acting on a beam are represented in SF and BM diagrams:

Shear force and bending moment diagrams for common loads

So how do we actually construct the SF and BM diagrams directly? The best way to explain is through an example.

*By the way, SF and BM diagram is probably the most important topic in this entire Statics course. You will be using a lot of it even in future courses (Solid Mechanics I and Solid Mechanics II), so learn it well!