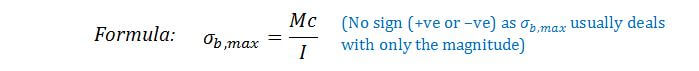engineering core courses

Solid Mechanics I
 Course homepage
Solid Mechanics I
 Course homepage
C4: Bending
4.1 Shear Force and Bending Moment Diagrams
- Theory - Example
4.2 Flexure Formula
- Theory - Example - Question 1 - Question 2 - Question 3

C4.2 Flexure Formula

Understanding the stresses caused by bending is crucial because materials fail faster under bending. Take for example a biscuit, you don’t pull it axially to break it, but instead you bend it to break it. That’s because bending stress is greater than axial stress for the same force magnitude applied.

Here, we learn the formula to quantify bending stress:


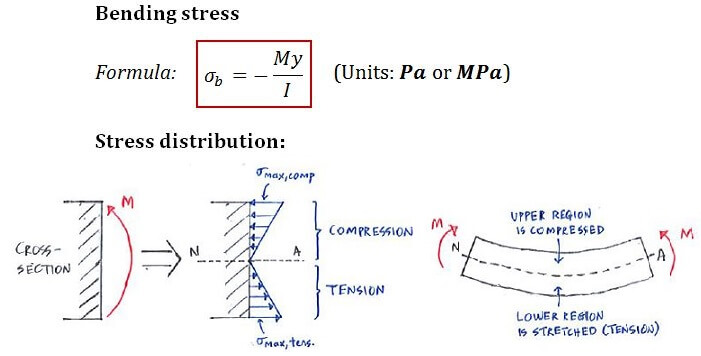
Bending stress or flexure formula and bending stress distribution
Note:
  • M is the internal bending moment at the region of interest (units: Nm). We can obtain this from the SFBM diagram.
  • y is the perpendicular distance from the neutral axis (units: m or mm)
  • I is the moment of inertia about the neutral-axis for the cross-section (units: m4 or mm4)
  • Sign: +ve for tension, -ve for compression.

C4.2 Flexure Formula

Understanding the stresses caused by bending is crucial because materials fail faster under bending. Take for example a biscuit, you don’t pull it axially to break it, but instead you bend it to break it. That’s because bending stress is greater than axial stress for the same force magnitude applied.

Here, we learn the formula to quantify bending stress:


Bending stress or flexure formula and bending stress distribution
Note:
  • M is the internal bending moment at the region of interest (units: Nm). We can obtain this from the SFBM diagram.
  • y is the perpendicular distance from the neutral axis (units: m or mm)
  • I is the moment of inertia about the neutral-axis for the cross-section (units: m4 or mm4)
  • Sign: +ve for tension, -ve for compression.

Notice that the higher the y the larger the bending stress. At ymax we have σmax. Similar to the torsion formula, we denote ymax as c:


Maximum bending stress or flexure formula

Sign convention

You might be wondering why is there a –ve sign in front of the bending stress formula. Here’s why:


Tension and compression in flexure formula

The –ve sign in the formula gives the correct sign to the compressive stress based on the +ve sign convention of M and y. Similarly in the bottom region, y is –ve, and therefore using the formula we get a +ve stress (tension) which is correct.

Let’s look at an example now.

Notice that the higher the y the larger the bending stress. At ymax we have σmax. Similar to the torsion formula, we denote ymax as c:


Maximum bending stress or flexure formula

Sign convention

You might be wondering why is there a –ve sign in front of the bending stress formula. Here’s why:


Tension and compression in flexure formula

The –ve sign in the formula gives the correct sign to the compressive stress based on the +ve sign convention of M and y. Similarly in the bottom region, y is –ve, and therefore using the formula we get a +ve stress (tension) which is correct.

Let’s look at an example now.

engineering core courses

COURSES FEATURES THE STORY CONTACT US ECC facebook link
engineering core courses