Without further ado, let’s look at the formula:

- V is the shear force acting on the cross-section (units: N)
- Q = Aȳ and it’s the same Q as in transverse shear (units: m3 or mm3)
- I is the moment of inertia (units: m4 or mm4)
- It’s pretty much the same as τ = VQ/It, except that the thickness τ is dropped out.
Shear flow direction and distribution
Another information of interest is how the shear actually “flows” in the cross-section. Knowing where the shear flow starts and ends will help us determine how we calculate our “Q” (Q = Aȳ) at the point of interest.
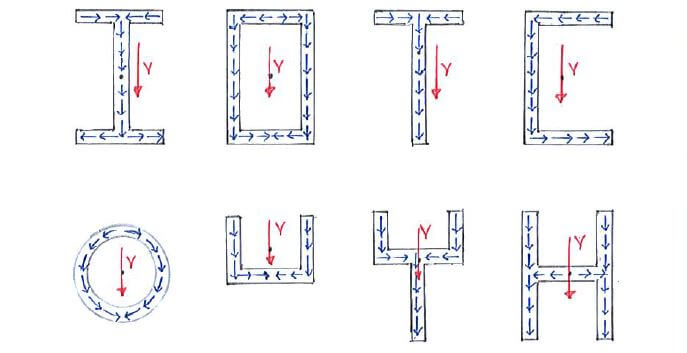
Here are two useful hints to help us determine our shear flow direction:
- The net effect of the shear flow will result in the shear force V acting on the cross-section. This means that the vertical regions of the cross-section should generally have q in the same direction as V.
- Shear flow q must be continuous regardless of the cross-section geometry.
Putting these 2 guidelines together, here are the shear flow distributions of some common cross-sections:
Shear force from shear flow
At the point where q starts in the cross-section, q = 0, but as it flows q gradually increases because Q = Aȳ goes up as well. An example of the q magnitude distribution for an I-section is shown below:
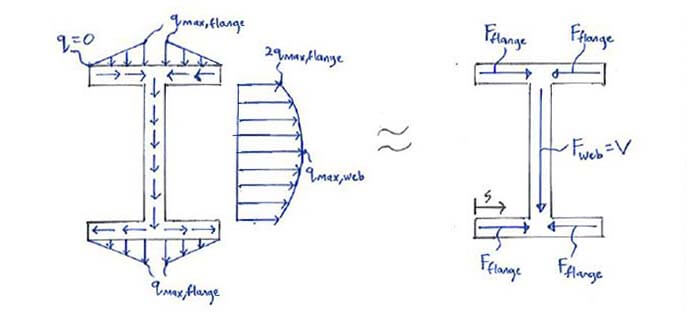
Using this information, we can actually work out the force caused by the shear flow for an arbitrary segment of the cross-section:

This might look difficult, but we’ll be looking at an example of this later in Question 3. For now, let’s look at a simple example.
Without further ado, let’s look at the formula:

- V is the shear force acting on the cross-section (units: N)
- Q = Aȳ and it’s the same Q as in transverse shear (units: m3 or mm3)
- I is the moment of inertia (units: m4 or mm4)
- It’s pretty much the same as τ = VQ/It, except that the thickness t is dropped out.
Shear flow direction and distribution
Another information of interest is how the shear actually “flows” in the cross-section. Knowing where the shear flow starts and ends will help us determine how we calculate our “Q” (Q = Aȳ) at the point of interest.
Here are two useful hints to help us determine our shear flow direction:
- The net effect of the shear flow will result in the shear force V acting on the cross-section. This means that the vertical regions of the cross-section should generally have q in the same direction as V.
- Shear flow q must be continuous regardless of the cross-section geometry.
Putting these 2 guidelines together, here are the shear flow distributions of some common cross-sections:

Shear force from shear flow
At the point where q starts in the cross-section, q = 0, but as it flows q gradually increases because Q = Aȳ goes up as well. An example of the q magnitude distribution for an I-section is shown below:

Using this information, we can actually work out the force caused by the shear flow for an arbitrary segment of the cross-section:

This might look difficult, but we’ll be looking at an example of this later in Question 3. For now, let’s look at a simple example.