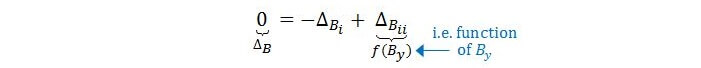Adding supports in this manner is actually good (even though its indeterminate), because it makes structures stronger. Therefore knowing how to analyse statically indeterminate beams/shafts will be important for you as future engineers.
In indeterminate scenarios we have more forces than necessary to ensure static equilibrium. To overcome this, we use the superposition method,
which states that the net displacement on a point is just the sum of the displacements due to the individual forces acting at that point.
Sounds complicated? Not to worry, let’s look at a simple example to understand this:

The beam above has an extra support at B which is redundant. To fully analyse the beam, we need to reactions Ay, By and Cy. Using our standard equations of equilibrium,
we can get Ay and Cy in terms of By but we still need to solve for By.
Here’s where superposition comes in. We isolate the support B as such:
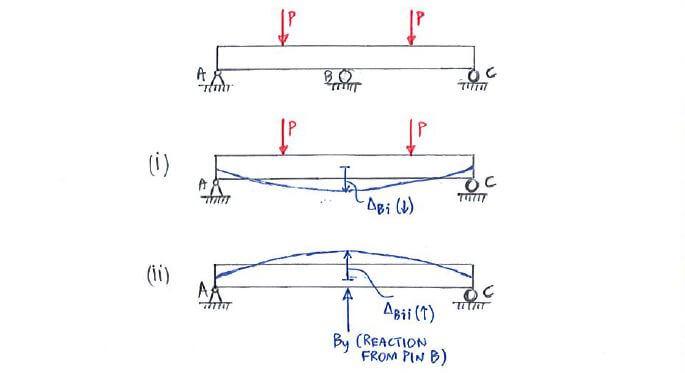
That is, for (i) we remove the redundant support at B and consider the resulting displacement (ΔBi↓). Then in (ii) we consider the displacement caused by the reaction By
(ΔBii↑).
Since in the real scenario there is a pin at B (i.e. ΔB = 0), we have our compatibility equation:
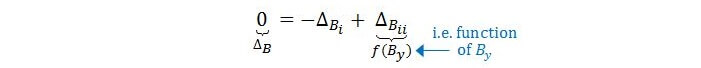
Using this, we can solve for By and then get our Ay and Cy.
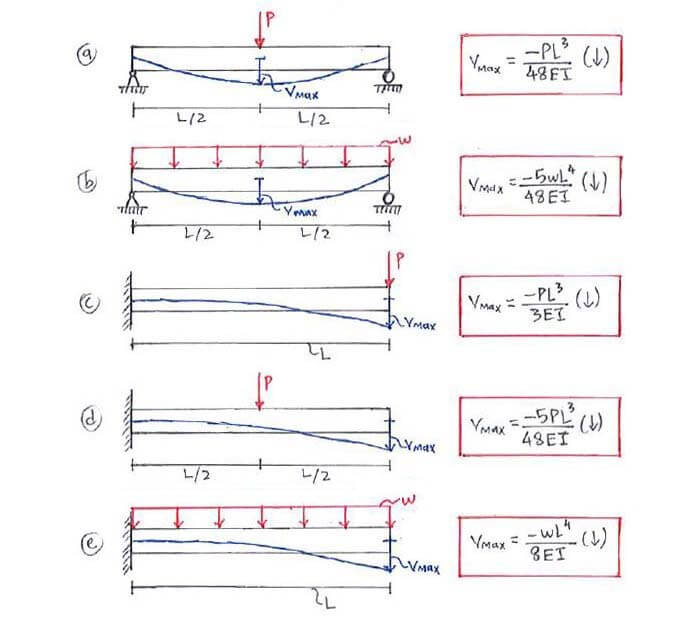
The displacements ΔBi↓ and ΔBii↓ can be obtained either using double integration or
virtual work. For simplicity, we provide here a list of displacement expressions for common loading conditions:
Alright! Looks like we’re ready. Let’s look at an example now.
Adding supports in this manner is actually good (even though its indeterminate), because it makes structures stronger. Therefore knowing how to analyse statically indeterminate beams/shafts will be important for you as future engineers.
In indeterminate scenarios we have more forces than necessary to ensure static equilibrium. To overcome this, we use the superposition method,
which states that the net displacement on a point is just the sum of the displacements due to the individual forces acting at that point.
Sounds complicated? Not to worry, let’s look at a simple example to understand this:

The beam above has an extra support at B which is redundant. To fully analyse the beam, we need to reactions Ay, By and Cy. Using our standard equations of equilibrium,
we can get Ay and Cy in terms of By but we still need to solve for By.
Here’s where superposition comes in. We isolate the support B as such:

That is, for (i) we remove the redundant support at B and consider the resulting displacement (ΔBi↓). Then in (ii) we consider the displacement caused by the reaction By
(ΔBii↑).
Since in the real scenario there is a pin at B (i.e. ΔB = 0), we have our compatibility equation:
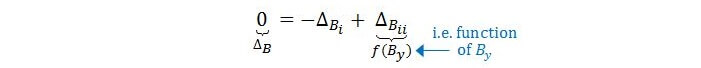
Using this, we can solve for By and then get our Ay and Cy.
The displacements ΔBi↓ and ΔBii↓ can be obtained either using double integration or
virtual work. For simplicity, we provide here a list of displacement expressions for common loading conditions:

Alright! Looks like we’re ready. Let’s look at an example now.