engineering core courses

Statics
 Course homepage
Statics
 Course homepage
C2: Free-Body Diagram and Equilibrium
2.1 Free-Body Diagram (FBD) and Supports
- Theory - Example - Question 1 - Question 2 - Question 3
2.2 Equations of Equilibrium
- Theory - Example - Question 1 - Question 2 - Question 3

C2.2 Equations of Equilibrium

When objects are stationary, they are in a state called static equilibrium. This means that they are not moving nor are they accelerating.

This is achieved when all action forces are balanced by reaction forces, i.e. when the sum of forces is equal to zero. In equation terms:

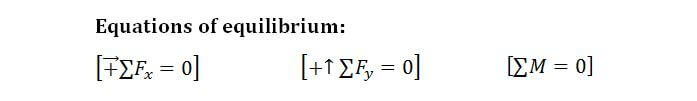
Formula for the three equations of equilibrium

These are the 3 fundamental statics equations, and they will help us determine the reaction forces necessary to keep a body in equilibrium under any action forces.

C2.2 Equations of Equilibrium

When objects are stationary, they are in a state called static equilibrium. This means that they are not moving nor are they accelerating.

This is achieved when all action forces are balanced by reaction forces, i.e. when the sum of forces is equal to zero. In equation terms:

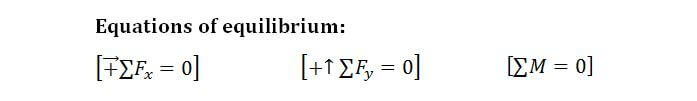
Formula for the three equations of equilibrium

These are the 3 fundamental statics equations, and they will help us determine the reaction forces necessary to keep a body in equilibrium under any action forces.

Here are some helpful hints when solving static questions using equations of equilibrium:

  • usually we draw the x-y axis on the side to define the +ve x and +ve y directions
  • this will be useful for you to ensure consistency of the +ve or –ve signs of the forces that you put in the equation of equilibrium, depending on the forces’ directions.

Let’s look at an example now.

Here are some helpful hints when solving static questions using equations of equilibrium:

  • usually we draw the x-y axis on the side to define the +ve x and +ve y directions
  • this will be useful for you to ensure consistency of the +ve or –ve signs of the forces that you put in the equation of equilibrium, depending on the forces’ directions.

Let’s look at an example now.

engineering core courses

COURSES FEATURES THE STORY CONTACT US ECC facebook link
engineering core courses