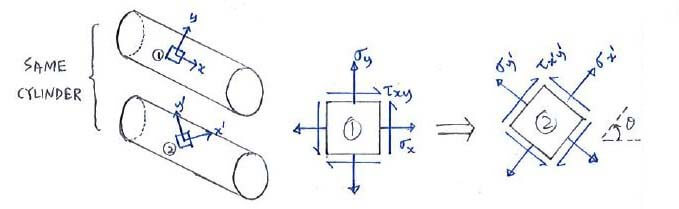
The stresses for element 1 are easy to obtain as we know our σhoop and σlong formulas from Chapter 6.1.
But what if we wanted to consider an element in the orientation of element 2? It’s the same cylindrical vessel experiencing the same load, except that we’re considering an element tilted by θ. How do we get the stress for this?
Well, here’s where our equations of plane-stress transformation come into play:

The equations are derived by considering the sum of forces of the tilted element together with the original element. We won’t be going through it; I suggest you read Chapter 9 of Hibbeler’s textbook.
To be completely honest, this subtopic is here for completeness sake. In practice we use Mohr’s circle, which is a more straightforward and easy approach to perform our stress-transformation.
But nonetheless here’s an example to help you see how the formulas are used.
The stresses for element 1 are easy to obtain as we know our σhoop and σlong formulas from Chapter 6.1.
But what if we wanted to consider an element in the orientation of element 2? It’s the same cylindrical vessel experiencing the same load, except that we’re considering an element tilted by θ. How do we get the stress for this?
Well, here’s where our equations of plane-stress transformation come into play:

The equations are derived by considering the sum of forces of the tilted element together with the original element. We won’t be going through it; I suggest you read Chapter 9 of Hibbeler’s textbook.
To be completely honest, this subtopic is here for completeness sake. In practice we use Mohr’s circle, which is a more straightforward and easy approach to perform our stress-transformation.
But nonetheless here’s an example to help you see how the formulas are used.