C8.2 Mohr’s Circle for Strain
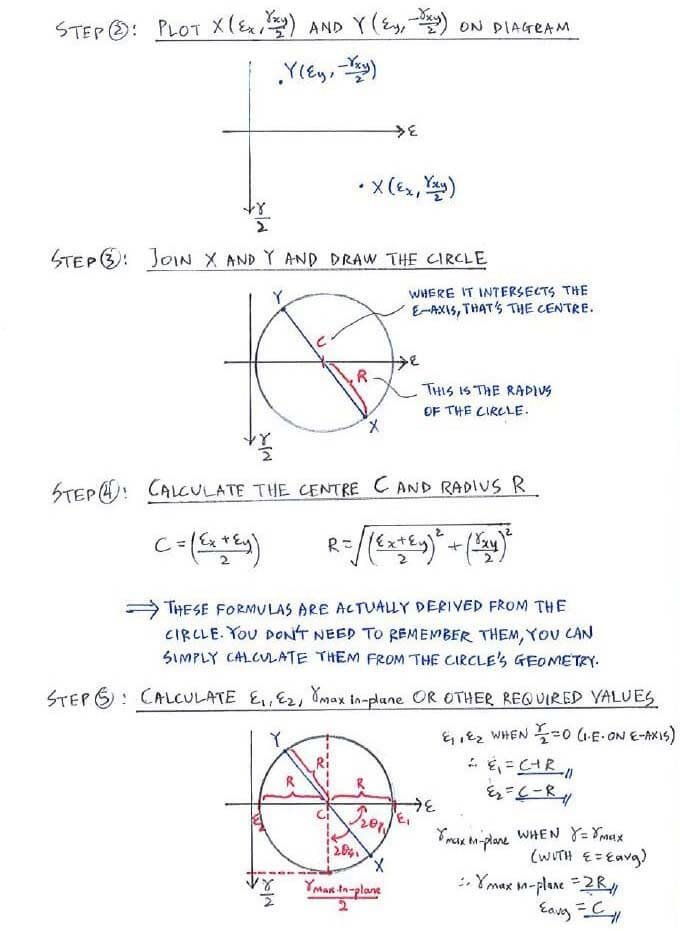
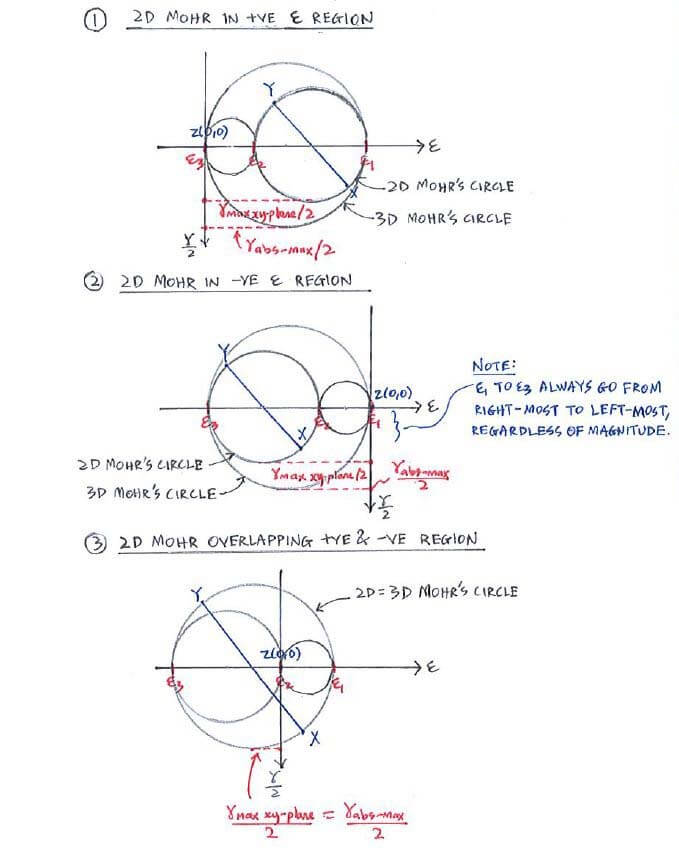
Like strain transformation, the Mohr’s circle for strain is just like the one for stress, except that σx, σy, τxy are converted to εx, εy, γxy/2 instead.
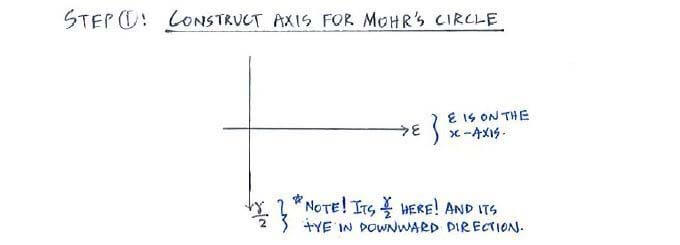
The construction steps are exactly the same as the Mohr’s circle for stress:
C8.2 Mohr’s Circle for Strain
Like strain transformation, the Mohr’s circle for strain is just like the one for stress, except that σx, σy, τxy are converted to εx, εy, γxy/2 instead.
The construction steps are exactly the same as the Mohr’s circle for stress: