σθ and σΦ – perpendicular stresses in shell structures
Shell structures experience loadings such as the internal pressure or the weight of the fluid it holds. These "action" loadings are resisted by the stresses that act along the thin-walled shells of the structure.
The general way of denoting the stresses along the shells is by the perpendicular σθ and σΦ, which act in the “θ” and “Φ” direction. We use a simple sphere to illustrate how σθ and σΦ acts and how rθ and rΦ are measured:
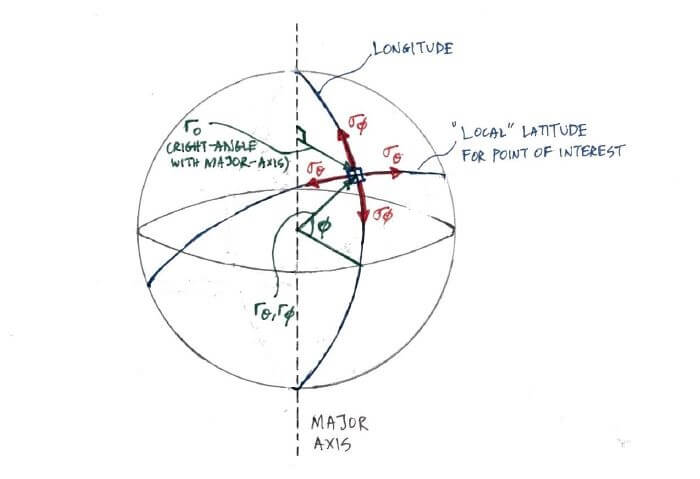
- rθ - radius of the arc that "sweeps" along the local latitude direction
- rΦ - radius of the arc that "sweeps" along the longitudinal direction
- ro - radius from the major-axis to the point of interest. The direction of the radius is always perpendicular to the major axis of the geometry.
- σθ - stress of the spherical shell acting in the local latitude direction from the point of interest
- σΦ - stress of the spherical shell acting in the longitudinal direction from the point of interest
- Φ measures the vertical angle along the longitudinal line, from the point of interest to the equator
We will be looking at how to define the directions of σθ, σΦ and rθ, rΦ for other shapes later.
Membrane stress equation
Based on the σθ and σΦ that we’ve just defined, the formula to solve for the stress is as follows:

This equation is usually used to solve for σθ. For σΦ, we solve it by using [+↑ΣFy = 0], which includes other y-forces such as pressure in the vessel and weight of the fluid contained.
We’ll see how this formula is used in the example shortly.
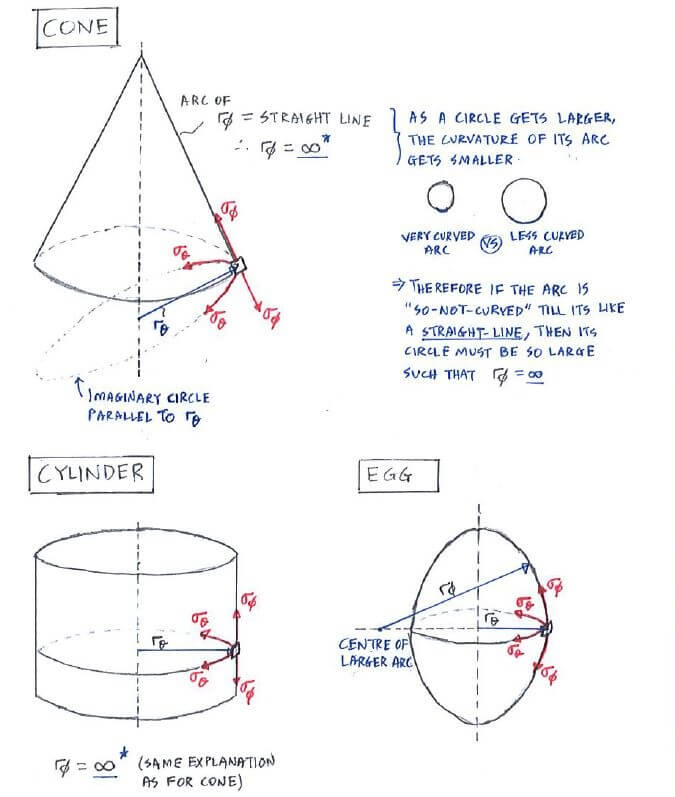
σθ, σΦ and rθ, rΦ for other shapes
Here we look at the σθ, σΦ and rθ, rΦ for shell structures with other shapes:
Procedure to solve
Problems from this chapter can be tricky, but if you follow the procedure below you can solve the problems easily and systematically:
- Get values for ro, rΦ, rθ, angle Φ, p, t (all input parameters)*
- [+↑ΣFy = 0], find σΦ
- Solve membrane stress equation, find σθ
- Final answers for σθ, σΦ, σr (principal stresses), or find pmax or tmin (depending on the question)
*Note: Sometimes pressure p or thickness t is what you need to find as the answer of the question.
Lots of theory covered so far! Let’s look at an example now.
σθ and σΦ – perpendicular stresses in shell structures
Shell structures experience loadings such as the internal pressure or the weight of the fluid it holds. These "action" loadings are resisted by the stresses that act along the thin-walled shells of the structure.
The general way of denoting the stresses along the shells is by the perpendicular σθ and σΦ, which act in the “θ” and “Φ” direction. We use a simple sphere to illustrate how σθ and σΦ acts and how rθ and rΦ are measured:

- rθ - radius of the arc that "sweeps" along the local latitude direction
- rΦ - radius of the arc that "sweeps" along the longitudinal direction
- ro - radius from the major-axis to the point of interest. The direction of the radius is always perpendicular to the major axis of the geometry.
- σθ - stress of the spherical shell acting in the local latitude direction from the point of interest
- σΦ - stress of the spherical shell acting in the longitudinal direction from the point of interest
- Φ measures the vertical angle along the longitudinal line, from the point of interest to the equator
We will be looking at how to define the directions of σθ, σΦ and rθ, rΦ for other shapes later.
Membrane stress equation
Based on the σθ and σΦ that we’ve just defined, the formula to solve for the stress is as follows:

This equation is usually used to solve for σθ. For σΦ, we solve it by using [+↑ΣFy = 0], which includes other y-forces such as pressure in the vessel and weight of the fluid contained.
We’ll see how this formula is used in the example shortly.
σθ, σΦ and rθ, rΦ for other shapes
Here we look at the σθ, σΦ and rθ, rΦ for shell structures with other shapes:

Procedure to solve
Problems from this chapter can be tricky, but if you follow the procedure below you can solve the problems easily and systematically:
- Get values for ro, rΦ, rθ, angle Φ, p, t (all input parameters)*
- [+↑ΣFy = 0], find σΦ
- Solve membrane stress equation, find σθ
- Final answers for σθ, σΦ, σr (principal stresses), or find pmax or tmin (depending on the question)
*Note: Sometimes pressure p or thickness t is what you need to find as the answer of the question.
Lots of theory covered so far! Let’s look at an example now.