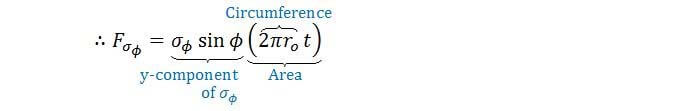σθ, σΦ
and rθ, rΦ definition
It might be hard to imagine how σθ, σΦ and rθ, rΦ
are defined for a toroidal shell, but as long as you follow the convention shown in the picture below you should be able to answer toroidal shell problems.
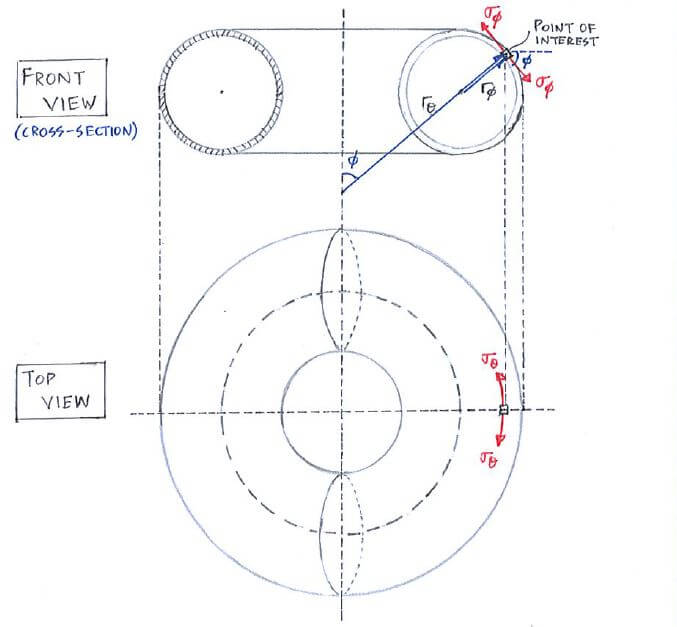
Sign conventions
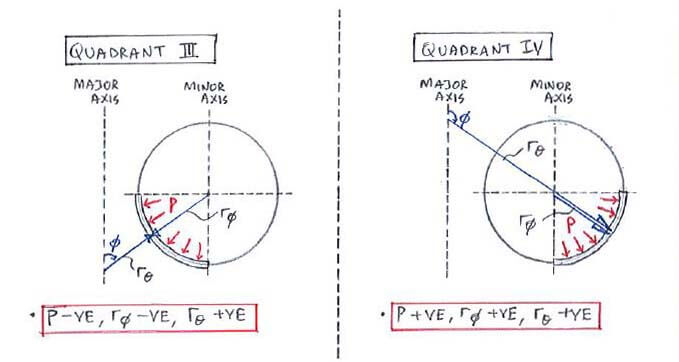
For toroidal shell problems you might be asked to find the stress in any of the 4 quadrants:
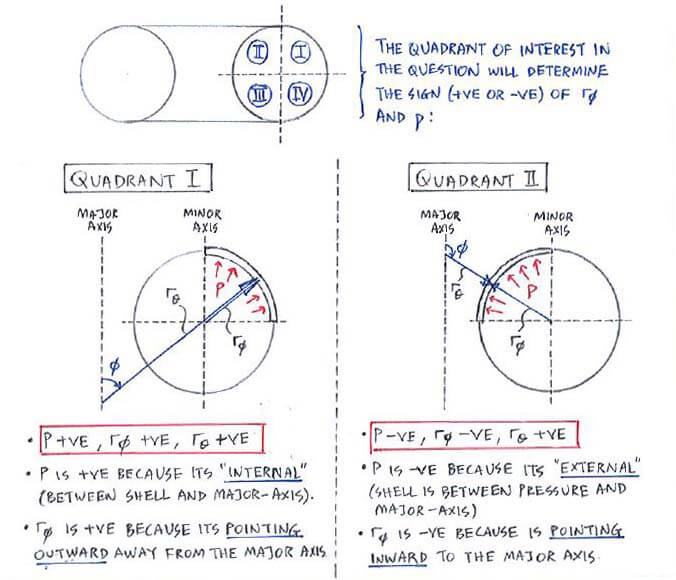
Using the same rules, we can work out the signs of rΦ and p for quadrants III and IV:
Calculating force for [+↑ΣFy = 0]
For the force due to pressure in the y-direction, we take the segment of the shell from the point of interest to where it ends at the minor-axis:
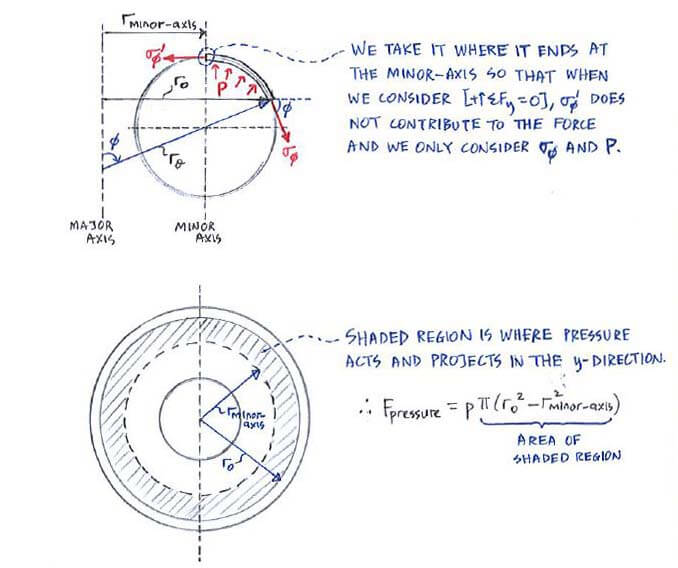
For σΦ, it acts on the thickness along the circumference with r = ro.
Since r >> t, we can approximate the area σΦ acts on as 2πrot:
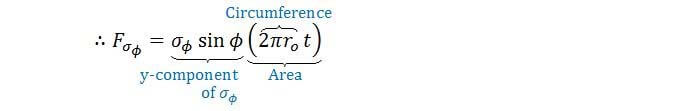
Let’s look at an example now.
σθ, σΦ
and rθ, rΦ definition
It might be hard to imagine how σθ, σΦ and rθ, rΦ
are defined for a toroidal shell, but as long as you follow the convention shown in the picture below you should be able to answer toroidal shell problems.

Sign conventions
For toroidal shell problems you might be asked to find the stress in any of the 4 quadrants:

Using the same rules, we can work out the signs of rΦ and p for quadrants III and IV:

Calculating force for [+↑ΣFy = 0]
For the force due to pressure in the y-direction, we take the segment of the shell from the point of interest to where it ends at the minor-axis:

For σΦ, it acts on the thickness along the circumference with r = ro.
Since r >> t, we can approximate the area σΦ acts on as 2πrot:
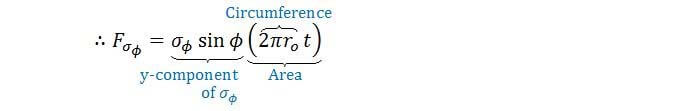
Let’s look at an example now.