Composite beams are usually beams with 2 or more materials joint together. For instance you might have a wooden beam covered with steel plates:
Composite beams are usually beams with 2 or more materials joint together. For instance you might have a wooden beam covered with steel plates:
Since the different materials in the beam are joint tightly together, it makes sense that the strain is continuous along the cross-section when its subjected to bending:
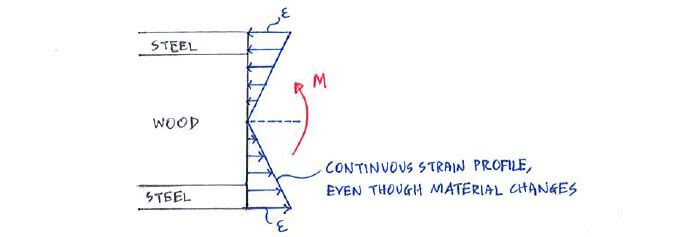
But if the Young’s modulus E of the materials are different, then based on σ = Eε it means the stress is not continuous along the cross-section.
How do we then calculate the bending stress in composite beams?
Well what we can do is to transform the material to have the same Young’s modulus as one another. We do so by “compacting” the material to make it “stiffer”, hence giving it a higher E:
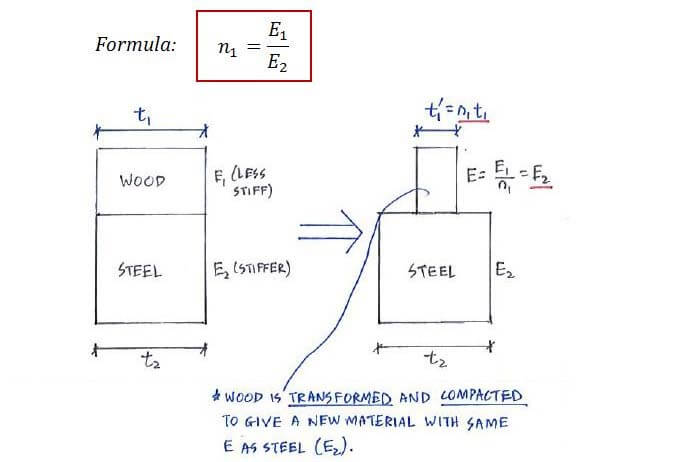
Once the composite beam is transformed to have the same E, we can apply the bending formula (σb = -My/I) directly to calculate our bending stress.
Finally once we have our bending stress distribution from the bending formula, we need to transform the wood back to its original state (“decompacting”). That would mean stretching the wood back to t1, but that would also mean the stress now is redistributed over a wider area, hence reducing its magnitude:
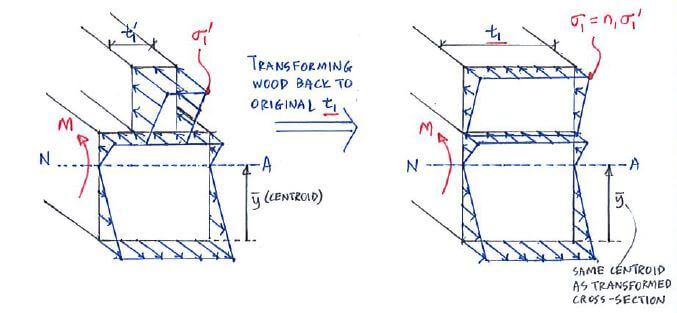
Now the transformation example shown previously was for the compacting (n1 < 1, E1 < E2), but we can apply the same method by expanding the material as well, to make it less stiff (n1 > 1, E1 > E2). The same procedure applies.
Let’s look at an example now.
Since the different materials in the beam are joint tightly together, it makes sense that the strain is continuous along the cross-section when its subjected to bending:
But if the Young’s modulus E of the materials are different, then based on σ = Eε it means the stress is not continuous along the cross-section.
How do we then calculate the bending stress in composite beams?
Well what we can do is to transform the material to have the same Young’s modulus as one another. We do so by “compacting” the material to make it “stiffer”, hence giving it a higher E:
Once the composite beam is transformed to have the same E, we can apply the bending formula (σb = -My/I) directly to calculate our bending stress.
Finally once we have our bending stress distribution from the bending formula, we need to transform the wood back to its original state (“decompacting”). That would mean stretching the wood back to t1, but that would also mean the stress now is redistributed over a wider area, hence reducing its magnitude:
Now the transformation example shown previously was for the compacting (n1 < 1, E1 < E2), but we can apply the same method by expanding the material as well, to make it less stiff (n1 > 1, E1 > E2). The same procedure applies.
Let’s look at an example now.