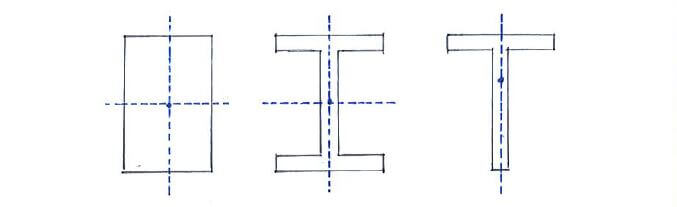
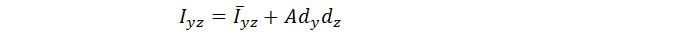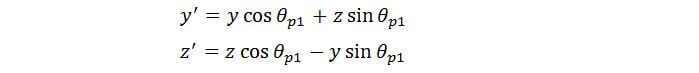What if we have a non-symmetrical cross-section? What happens? Can we still apply the bending formula directly?
The answer is no, because the bending formula only works with principal moments of inertia. Non-symmetrical cross sections have what we call the product of inertia Iyz
(analogous to τxy), and we need to transform the moment of inertia such that Iy'z' = 0.
From this, we then get our principal moments of inertia I1, I2 (analogous to σ1, σ2).
And yes, you’ve guessed it, we use the Mohr’s circle to do the transformation =) But first, let’s look at the product of inertia.
Product of inertia, Iyz
The definition of Iyz is:

You probably won’t need to calculate this; suffice for you to know that as long as there is an axis of symmetry, Iyz = 0.
We also have the parallel-axis theorem for Iyz:
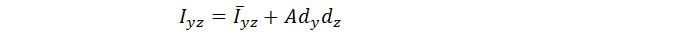
Consider the following cross-section. We're going to attempt to calculate its product of inertia:
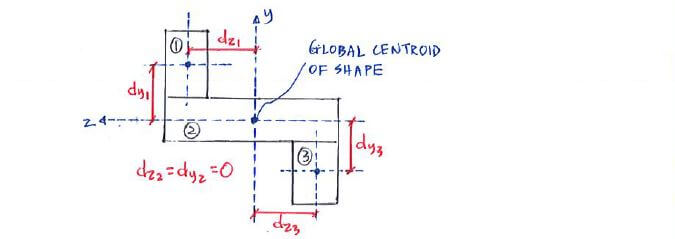
Since the individual shapes 1, 2, 3 all have a local axis of symmetry, their local products of inertia are zero
(Iyz1 = Iyz2 = Iyz3 = 0).
Therefore the product of inertia for the shape is:

Principal moment of inertia
The construction process is exactly the same as the standard Mohr’s Circle in Solid Mechanics I, except that:
-
initial coordinates are Y (Iy, Iyz) and Z (Iz, -Iyz).
-
the Iyz-axis is +ve upwards
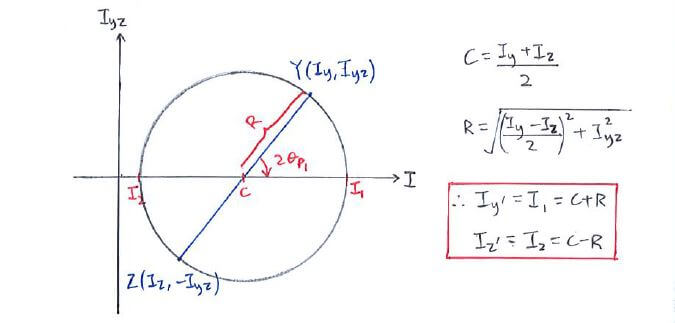
These principal moments of inertia Iy' and Iz' can then be used in the bending stress formula.
However due to the rotation of the axes (y−z to y'−z' at θ = θp1),
the coordinates of the point of interest with respect to the new axes y'−z' will also change.
Calculating new coordinates y' and z'
Let’s look at a sample cross-section to derive the formula for y' and z':
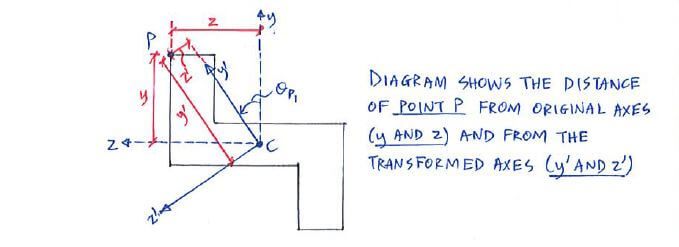
Look’s complex? Let’s try to break it down:
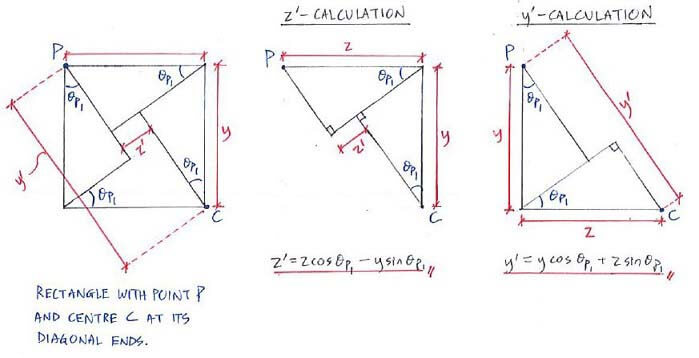
Complex? Don’t worry, just remember:
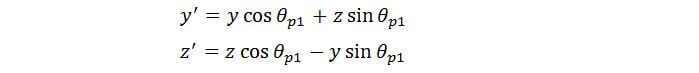
If θp1 is clockwise (CW), just plug it into the equation as -θp1.
Let’s look at an example now.
What if we have a non-symmetrical cross-section? What happens? Can we still apply the bending formula directly?

The answer is no, because the bending formula only works with principal moments of inertia. Non-symmetrical cross sections have what we call the product of inertia Iyz
(analogous to τxy), and we need to transform the moment of inertia such that Iy'z' = 0.
From this, we then get our principal moments of inertia I1, I2 (analogous to σ1, σ2).
And yes, you’ve guessed it, we use the Mohr’s circle to do the transformation =) But first, let’s look at the product of inertia.
Product of inertia, Iyz
The definition of Iyz is:

You probably won’t need to calculate this; suffice for you to know that as long as there is an axis of symmetry, Iyz = 0.
We also have the parallel-axis theorem for Iyz:
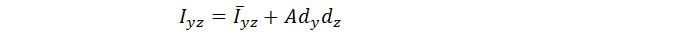
Consider the following cross-section. We're going to attempt to calculate its product of inertia:

Since the individual shapes 1, 2, 3 all have a local axis of symmetry, their local products of inertia are zero
(Iyz1 = Iyz2 = Iyz3 = 0).
Therefore the product of inertia for the shape is:

Principal moment of inertia
The construction process is exactly the same as the standard Mohr’s Circle in Solid Mechanics I, except that:
-
initial coordinates are Y (Iy, Iyz) and Z (Iz, -Iyz).
-
the Iyz-axis is +ve upwards

These principal moments of inertia Iy' and Iz' can then be used in the bending stress formula.
However due to the rotation of the axes (y−z to y'−z' at θ = θp1),
the coordinates of the point of interest with respect to the new axes y'−z' will also change.
Calculating new coordinates y' and z'
Let’s look at a sample cross-section to derive the formula for y' and z':

Look’s complex? Let’s try to break it down:

Complex? Don’t worry, just remember:
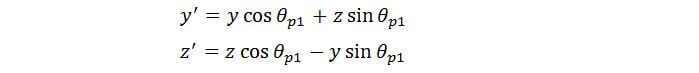
If θp1 is clockwise (CW), just plug it into the equation as -θp1.
Let’s look at an example now.