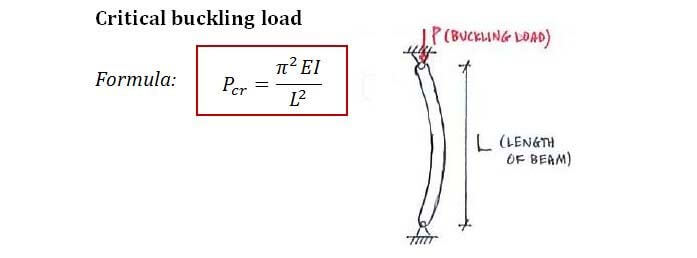
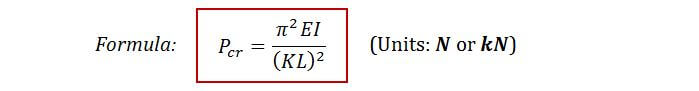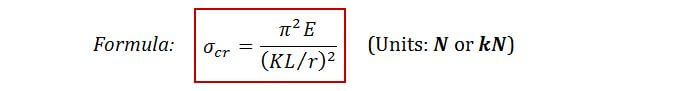Slender members experience a mode of failure called buckling. Therefore to design these slender members for safety we need to understand how to calculate the critical buckling load, which is what the Euler’s buckling formula is about.
Let’s look at the formula:
 Note:
Note:
-
Pcr is the critical buckling load (units: N or kN)
-
E is the Young’s modulus (units: GPa)
-
I is the moment of inertia that resists the direction of buckling (units: m4 or mm4)
-
L is the length of the slender members (units: m)
This formula only works when the material is still within its elastic limit. Also, the formula given above assumes that the slender member is pinned at both ends.
But what if it isn’t? What if it has fixed-pin ends? Well, we consider the effective length where the slender member is effectively double-pin ended:
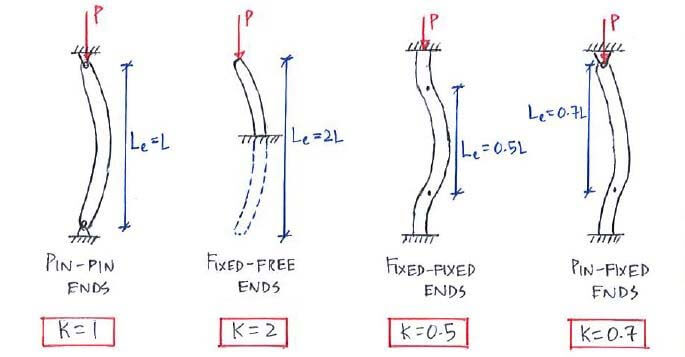
K in the figure above is the effective length factor. Now, we generalise our buckling formula to account for all scenarios:
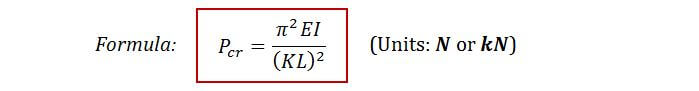
Sometimes you might also be asked to calculate the critical buckling stress. To do this, all you do is take σcr = Pcr/A (A = cross-sectional area). After rearranging, you’ll end up with a fancy formula:
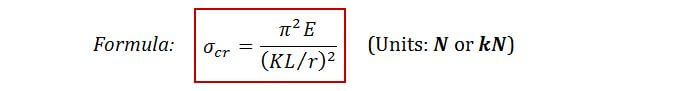 where:
where:
-
r is the radius of gyration (r=√I/A) (units: m or mm)
-
KL/r is called the slenderness ratio: the higher it is, the more “slender” the member is, which makes it easier to buckle (when KL/r ↑, σcr ↓ i.e. critical stress before buckling reduces).
Let’s look at how to use our Euler's formula!
Slender members experience a mode of failure called buckling. Therefore to design these slender members for safety we need to understand how to calculate the critical buckling load, which is what the Euler’s buckling formula is about.
Let’s look at the formula:
 Note:
Note:
-
Pcr is the critical buckling load (units: N or kN)
-
E is the Young’s modulus (units: GPa)
-
I is the moment of inertia that resists the direction of buckling (units: m4 or mm4)
-
L is the length of the slender members (units: m)
This formula only works when the material is still within its elastic limit. Also, the formula given above assumes that the slender member is pinned at both ends.
But what if it isn’t? What if it has fixed-pin ends? Well, we consider the effective length where the slender member is effectively double-pin ended:

K in the figure above is the effective length factor. Now, we generalise our buckling formula to account for all scenarios:
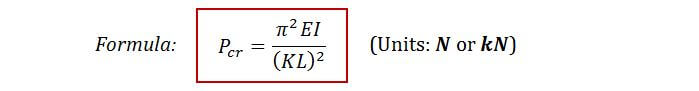
Sometimes you might also be asked to calculate the critical buckling stress. To do this, all you do is take σcr = Pcr/A (A = cross-sectional area). After rearranging, you’ll end up with a fancy formula:
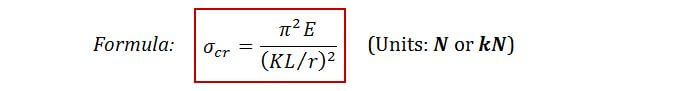 where:
where:
-
r is the radius of gyration (r=√I/A) (units: m or mm)
-
KL/r is called the slenderness ratio: the higher it is, the more “slender” the member is, which makes it easier to buckle (when KL/r ↑, σcr ↓ i.e. critical stress before buckling reduces).
Let’s look at how to use our Euler's formula!