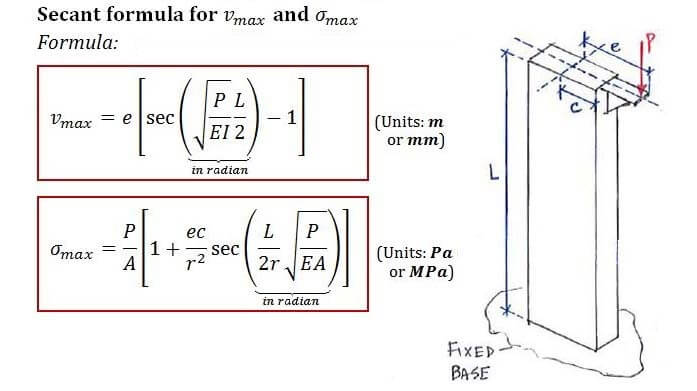
C5.2 Secant Formula

In the Euler’s buckling formula we assume that the load P acts through the centroid of the cross-section. However in reality this might not always be the case: the load P might be applied at an offset, or the slender member might not be completely straight.

To account for this, we assume that the load P is applied at a certain distance e (e for eccentricity) away from the centroid. This then would obviously change the way we calculate our buckling load, which is what the secant formula is for.

We use the secant formula to calculate the maximum deflection ν_max and maximum stress σ_max due to an eccentric load:

C5.2 Secant Formula

In the Euler’s buckling formula we assume that the load P acts through the centroid of the cross-section. However in reality this might not always be the case: the load P might be applied at an offset, or the slender member might not be completely straight.

To account for this, we assume that the load P is applied at a certain distance e (e for eccentricity) away from the centroid. This then would obviously change the way we calculate our buckling load, which is what the secant formula is for.

We use the secant formula to calculate the maximum deflection ν_max and maximum stress σ_max due to an eccentric load:

Secant formula

Note:

e is the eccentricity of the load, i.e. the distance of P away from the centroid (units: m or mm)
c is the maximum radius (the same c in maximum bending stress) where maximum compression occurs (units: m or mm)
A is the cross-sectional area (units: m² or mm²)
P is the buckling load applied (units: N or kN)
E, I, L have the same meaning as in the Euler’s formula (Young’s modulus, moment of inertia, length)
r is the radius of gyration (r=√I/A) (units: m or mm)

While the formula is complex, questions from this subtopic are usually very straight-forward. You only need to note that the expression within the secant term (sec [...]) is in radians. (Btw sec θ = 1/cos θ)

Let’s look at an example now.

Secant formula

Note:

e is the eccentricity of the load, i.e. the distance of P away from the centroid (units: m or mm)
c is the maximum radius (the same c in maximum bending stress) where maximum compression occurs (units: m or mm)
A is the cross-sectional area (units: m² or mm²)
P is the buckling load applied (units: N or kN)
E, I, L have the same meaning as in the Euler’s formula (Young’s modulus, moment of inertia, length)
r is the radius of gyration (r=√I/A) (units: m or mm)

While the formula is complex, questions from this subtopic are usually very straight-forward. You only need to note that the expression within the secant term (sec [...]) is in radians. (Btw sec θ = 1/cos θ)

Let’s look at an example now.