engineering core courses

Solid Mechanics II
 Course homepage
Solid Mechanics II
 Course homepage
C6: Energy Methods
6.1 Elastic Strain Energy for Various Loadings
- Theory - Example
6.2 Conservation of Energy
- Theory - Example - Question 1 - Question 2 - Question 3
6.3 Virtual Work
- Theory - Example - Question 1 - Question 2 - Question 3
6.4 Castigliano’s Theorem
- Theory - Example - Question 1

C6.2 Conservation of Energy

In Chapter 9 of Solid Mechanics I, we looked at calculating the displacement and slope using the double integration method as well as the Macaulay’s function.

Here we present another method (arguably simpler) to work out our displacement and slope: conservation of energy. Here’s the equation:

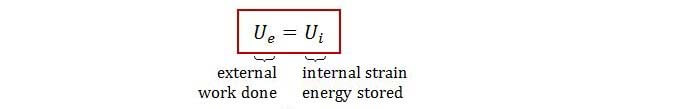
Conservation of energy equation to calculate displacement

Basically the equation states that the internal strain energy in the material must be “inputted” by the external work done from the action force. And the external work done is easy enough to calculate:

External work done formula for displacement and slope

C6.2 Conservation of Energy

In Chapter 9 of Solid Mechanics I, we looked at calculating the displacement and slope using the double integration method as well as the Macaulay’s function.

Here we present another method (arguably simpler) to work out our displacement and slope: conservation of energy. Here’s the equation:

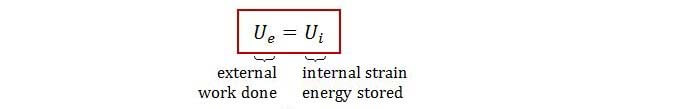
Conservation of energy equation to calculate displacement

Basically the equation states that the internal strain energy in the material must be “inputted” by the external work done from the action force. And the external work done is easy enough to calculate:

External work done formula for displacement and slope

If we equate Ue with our internal strain energy Ui (which we’ve worked out how to calculate previously), we can get our displacement and slope! Simple isn’t it!

The questions we’ll be looking at will mainly deal with trusses or beams, which is the most common type of question you will encounter.

Let’s look at an example now.

If we equate Ue with our internal strain energy Ui (which we’ve worked out how to calculate previously), we can get our displacement and slope! Simple isn’t it!

The questions we’ll be looking at will mainly deal with trusses or beams, which is the most common type of question you will encounter.

Let’s look at an example now.

engineering core courses

COURSES FEATURES THE STORY CONTACT US ECC facebook link
engineering core courses