Ever notice those triangular network of metal frames when you drive past a bridge or walk under a roof?
Ever notice those triangular network of metal frames when you drive past a bridge or walk under a roof?
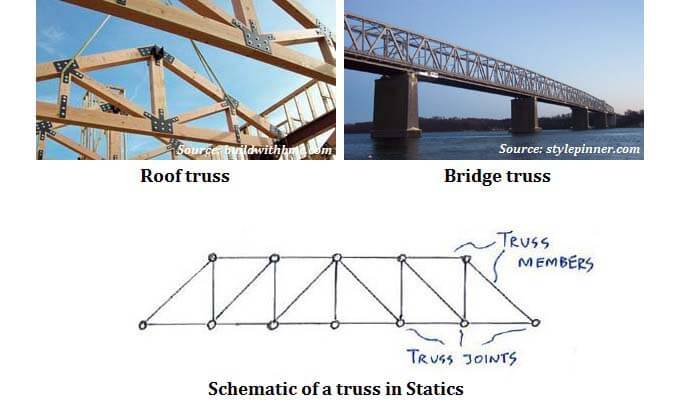
These are what we call trusses, and they play an extremely important role in ensuring the stability of structures. As such, analysing and designing such structures is important for all you budding engineers.
In this Statics course we will only be considering 2D trusses of plane-trusses. In trusses, we essentially have many individual truss members connected at joints.
Each truss member can be assumed to be two-force members, with only normal forces acting internally within each member without any bending moment. These internal forces can be treated as forces exerted by the truss members, acting from the tips:
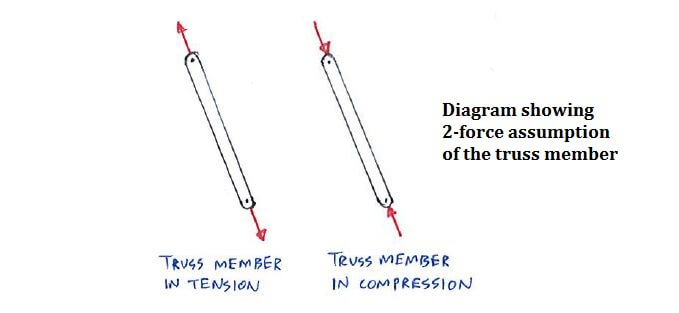
The two-force member assumption is not made randomly, but can actually be proven to be valid. We show you the proof here.
If you were tasked to design a truss structure, how would you check whether the number of truss members in your design is insufficient (causing the truss to collapse) or excessive (resulting in overdesign)?
There is a simply formula to check this:
Consider the following truss configurations that illustrate the scenarios of being statically determinate or indeterminate:
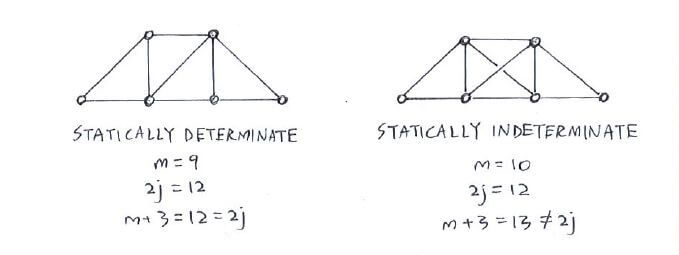
Observations:
Okay! That’s probably enough background information on trusses. Let’s move on to analysing them, starting with the method of joints.
These are what we call trusses, and they play an extremely important role in ensuring the stability of structures. As such, analysing and designing such structures is important for all you budding engineers.
In this Statics course we will only be considering 2D trusses of plane-trusses. In trusses, we essentially have many individual truss members connected at joints.
Each truss member can be assumed to be two-force members, with only normal forces acting internally within each member without any bending moment. These internal forces can be treated as forces exerted by the truss members, acting from the tips:
The two-force member assumption is not made randomly, but can actually be proven to be valid. We show you the proof here.
If you were tasked to design a truss structure, how would you check whether the number of truss members in your design is insufficient (causing the truss to collapse) or excessive (resulting in overdesign)?
There is a simply formula to check this:
Consider the following truss configurations that illustrate the scenarios of being statically determinate or indeterminate:
Observations:
Okay! That’s probably enough background information on trusses. Let’s move on to analysing them, starting with the method of joints.