You will be encountering two-force members not only in trusses, so it’s good to know what they are.
Let’s consider a truss member that is pinned at both ends. The FBD might look something like this:
You will be encountering two-force members not only in trusses, so it’s good to know what they are.
Let’s consider a truss member that is pinned at both ends. The FBD might look something like this:
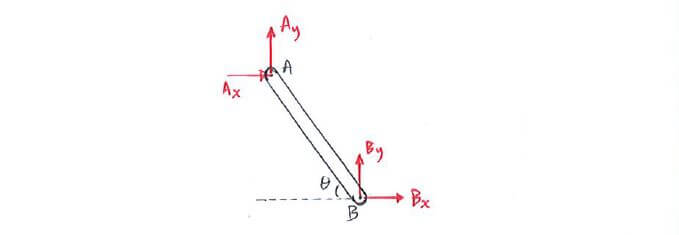
Since it’s a truss member that is supporting another structure, it should be in static equilibrium. Let’s try using the equations of equilibrium to solve for the forces at A and B:
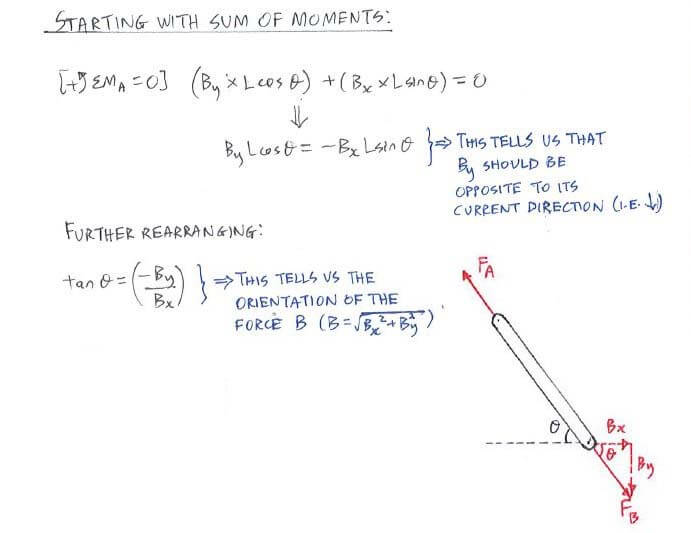
Did you notice that the resultant force at B is parallel to the member’s angle orientation? And if you solve for [ΣFx = 0] and [ΣFy = 0], you will get the resultant force at A such that it is equal and but opposite to B, as shown in the figure above.
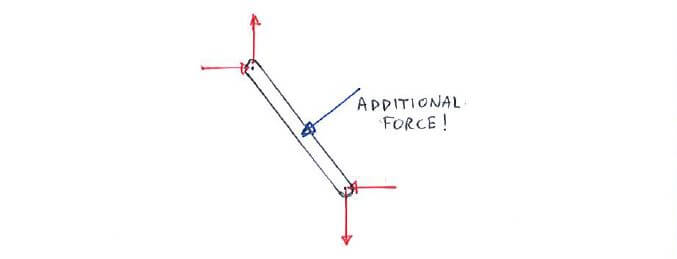
Note however, that when an additional force acts on the truss, the two-force effect is no longer valid. This is what we call a multi-force member, which will be covered in Chapter 3.4.
Now, back to the main theory on trusses. Let’s move on to the method of joints.
Since it’s a truss member that is supporting another structure, it should be in static equilibrium. Let’s try using the equations of equilibrium to solve for the forces at A and B:
Did you notice that the resultant force at B is parallel to the member’s angle orientation? And if you solve for [ΣFx = 0] and [ΣFy = 0], you will get the resultant force at A such that it is equal and but opposite to B, as shown in the figure above.
Note however, that when an additional force acts on the truss, the two-force effect is no longer valid. This is what we call a multi-force member, which will be covered in Chapter 3.4.
Now, back to the main theory on trusses. Let’s move on to the method of joints.