C1.2 Deformation and Strain

The importance of deformation

It is important to quantify the deformation of structures under loading to ensure it meets design specifications. For instance, you wouldn’t want the Sydney Harbour Bridge to be sagging by 5 m when cars pass through it! Might seem like an exaggeration, but you get the idea.

Deformation must also be considered relative to its own length. A 10 mm deformation in a rod might not seem big but if the rod’s original length is 20 mm, then it’s a 50% relative deformation! Similarly a 50 mm deflection in a beam might seem huge but if the beam is 15 m in length, then the deflection is acceptable.

The concept of “relative deformation” is what we call strain. We will consider both normal and shear strains.

C1.2 Deformation and Strain

The importance of deformation

It is important to quantify the deformation of structures under loading to ensure it meets design specifications. For instance, you wouldn’t want the Sydney Harbour Bridge to be sagging by 5 m when cars pass through it! Might seem like an exaggeration, but you get the idea.

Deformation must also be considered relative to its own length. A 10 mm deformation in a rod might not seem big but if the rod’s original length is 20 mm, then it’s a 50% relative deformation! Similarly a 50 mm deflection in a beam might seem huge but if the beam is 15 m in length, then the deflection is acceptable.

The concept of “relative deformation” is what we call strain. We will consider both normal and shear strains.

Normal strain

Consider a stretched rod as follows:

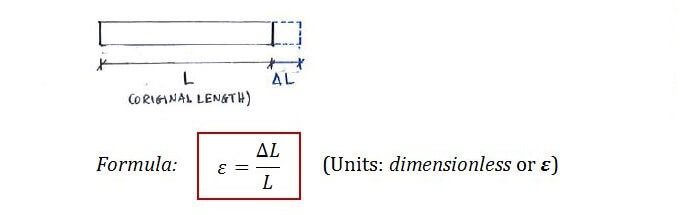
Normal Strain formula

Note:

To prevent confusion with other dimensionless parameters, we use “ε” as the unit to denote that it’s strain
Some textbooks also use m/m or mm/mm.
Sign: +ve for tensile strain, -ve for compressive strain

Shear strain

Shear strain is trickier. Rather than considering the change in length, we look at the “tilt” of the body under a shear load:

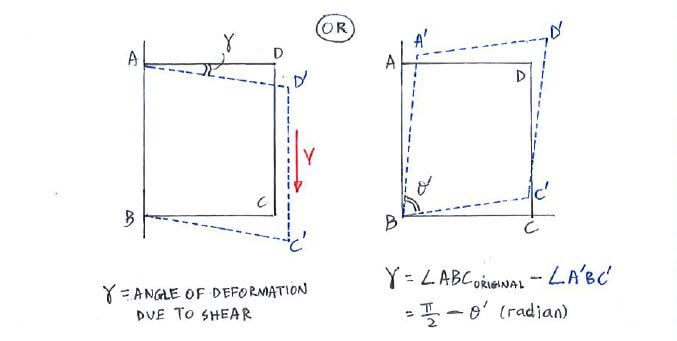
Shear Strain formula

Note:

Shear strain has the units of rad or radian
2 ways of calculating shear strain are presented above, but they are effectively the same
Sign: +ve or –ve does not matter now, but will be important when we look at strain transformation

Let’s look at an example now.

Normal strain

Consider a stretched rod as follows:

Normal Strain formula

Note:

To prevent confusion with other dimensionless parameters, we use “ε” as the unit to denote that it’s strain
Some textbooks also use m/m or mm/mm.
Sign: +ve for tensile strain, -ve for compressive strain

Shear strain

Shear strain is trickier. Rather than considering the change in length, we look at the “tilt” of the body under a shear load:

Shear Strain formula

Note:

Shear strain has the units of rad or radian
2 ways of calculating shear strain are presented above, but they are effectively the same
Sign: +ve or –ve does not matter now, but will be important when we look at strain transformation

Let’s look at an example now.