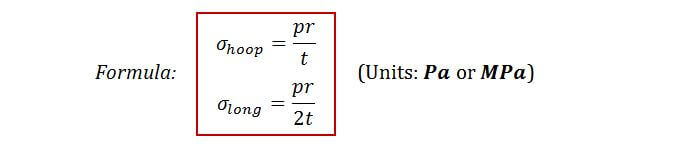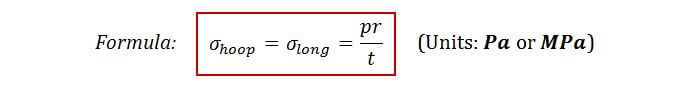The thin-walled pressure vessel analysis is formulated based on the assumption that the vessels fulfil the criteria r/t ≤ 10, i.e. the vessel is sufficiently thin with respect to its radius.
Here we look at the 2 most common types of vessels:
-
Cylindrical vessels
-
Spherical vessels
Cylindrical vessels
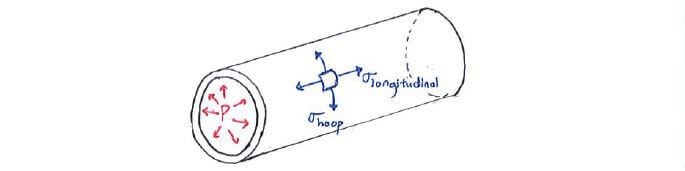
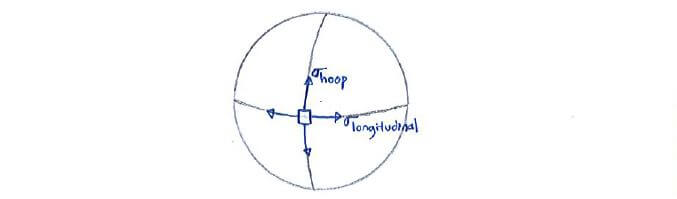
Let’s look at a cylindrical vessel. If we consider a tiny element on the vessel’s shell, we can split the stress into the components acting in the longitudinal (axial) direction and the hoop or circumferential direction.
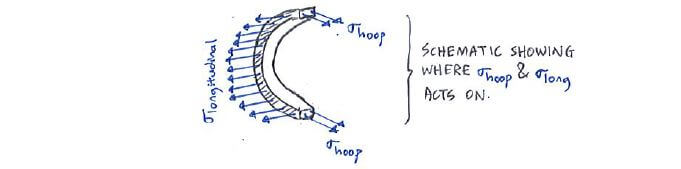
To give you a better understanding on how these stresses act, we dissect the vessel:
Now that we know the stress components, let’s look at the formula to calculate these:
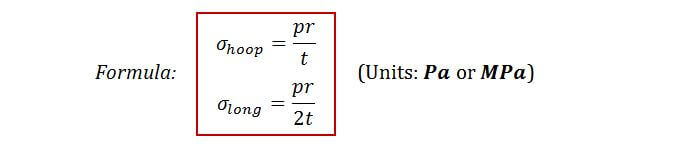 Note:
Note:
-
p is the pressure in the cylindrical vessel (units: Pa or MPa)
-
r is the internal radius of the vessel (units: m or mm)
-
t is the thickness of the vessel (units: m or mm)
-
σlong and σhoop are always +ve if the pressure acts from inside the vessel, and is –ve if p acts from outside the vessel.
-
If the cylinder is open-ended, σlong = 0; since there are no “caps” resisting the pressure, there will be no “pull” in the longitudinal direction and so σlong = 0.
Spherical vessels
For a spherical vessel, the curvature is constant throughout the entire sphere and therefore σlong and σhoop are the same.
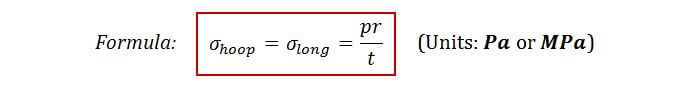
Radial stress
The 3rd stress component in pressure vessels is the radial stress. It is basically the normal stress acting in the radial direction due to the pressure. It’s the same as you using your palm to press against the wall: you feel the compressive effect from the normal stress.
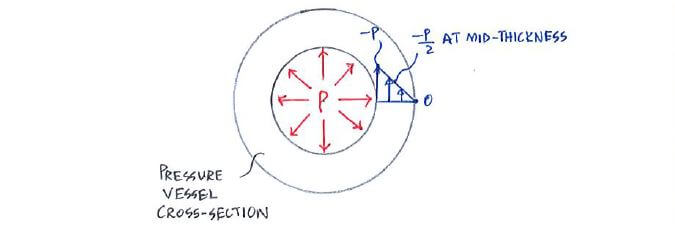
The exact theory for the radial stress distribution is complex, but we estimate it as:

Let’s look at an example now.
The thin-walled pressure vessel analysis is formulated based on the assumption that the vessels fulfil the criteria r/t ≤ 10, i.e. the vessel is sufficiently thin with respect to its radius.
Here we look at the 2 most common types of vessels:
-
Cylindrical vessels
-
Spherical vessels
Cylindrical vessels

Let’s look at a cylindrical vessel. If we consider a tiny element on the vessel’s shell, we can split the stress into the components acting in the longitudinal (axial) direction and the hoop or circumferential direction.
To give you a better understanding on how these stresses act, we dissect the vessel:

Now that we know the stress components, let’s look at the formula to calculate these:
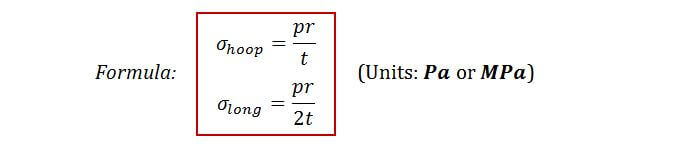 Note:
Note:
-
p is the pressure in the cylindrical vessel (units: Pa or MPa)
-
r is the internal radius of the vessel (units: m or mm)
-
t is the thickness of the vessel (units: m or mm)
-
σlong and σhoop are always +ve if the pressure acts from inside the vessel, and is –ve if p acts from outside the vessel.
-
If the cylinder is open-ended, σlong = 0; since there are no “caps” resisting the pressure, there will be no “pull” in the longitudinal direction and so σlong = 0.
Spherical vessels

For a spherical vessel, the curvature is constant throughout the entire sphere and therefore σlong and σhoop are the same.
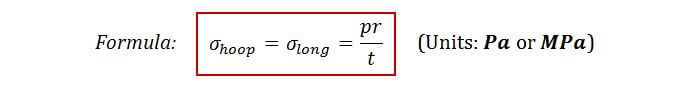
Radial stress
The 3rd stress component in pressure vessels is the radial stress. It is basically the normal stress acting in the radial direction due to the pressure. It’s the same as you using your palm to press against the wall: you feel the compressive effect from the normal stress.

The exact theory for the radial stress distribution is complex, but we estimate it as:

Let’s look at an example now.