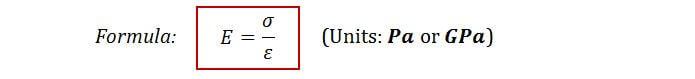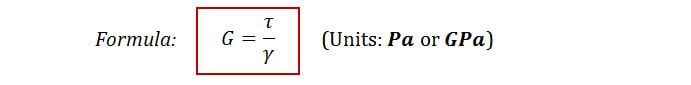engineering core courses

Solid Mechanics I
 Course homepage
Solid Mechanics I
 Course homepage
C1: Stress, Strain and Mechanical Properties
1.1 Normal and Shear Stress
- Theory - Example - Question 1 - Question 2 - Question 3
1.2 Deformation and Strain
- Theory - Example 1 - Example 2 - Question 1 - Question 2
1.3 Mechanical Properties of Materials
- Theory

C1.3 Mechanical Properties of Materials

In this subtopic, we will be looking at a few very important material properties that will be used throughout Solid Mechanics. But first, a quick recap on the stress-strain diagram.

Stress-strain (σ-ε) diagram

stress-strain diagram showing elastic region, plastic region, yield stress, and ultimate tensile stress
Note:
  • σy is the yield stress, σUTS is the ultimate tensile stress.
  • Material strains linearly until σy, and behaves elastically (i.e. it will return to its original shape when load is removed).
  • After σy, non-linear strain occurs and the deformation is plastic (i.e. deformation is permanent and it will not return to original shape).
  • After reaching σUTS, failure begins & necking ensues, and finally the material fractures and breaks into 2.
  • The gradient of the elastic region is what we call the Young’s modulus.

C1.3 Mechanical Properties of Materials

In this subtopic, we will be looking at a few very important material properties that will be used throughout Solid Mechanics. But first, a quick recap on the stress-strain diagram.

Stress-strain (σ-ε) diagram

stress-strain diagram showing elastic region, plastic region, yield stress, and ultimate tensile stress
Note:
  • σy is the yield stress, σUTS is the ultimate tensile stress.
  • Material strains linearly until σy, and behaves elastically (i.e. it will return to its original shape when load is removed).
  • After σy, non-linear strain occurs and the deformation is plastic (i.e. deformation is permanent and it will not return to original shape).
  • After reaching σUTS, failure begins & necking ensues, and finally the material fractures and breaks into 2.
  • The gradient of the elastic region is what we call the Young’s modulus.

Young’s modulus, E

Young's modulus formula
Note:
  • E measures the stiffness of the material. The higher the E, the less it strains under the same stress.
  • E is usually constant for the same material (e.g. Esteel = 200 GPa), so if we know the σ we can find ε using E, and vice-versa
  • The magnitude of E is usually very large, and GPa (109) is commonly used.
  • In experiments, stress is usually obtained by measuring strain using strain rosettes, and then converted to stress via E.

Poisson’s ratio, ν

Poisson ratio deformation effect

Have you ever noticed that, when you stretch anything (say a rubber block), part of the material actually thins or necks? That’s because the material needs to be redistributed to allow it to stretch. The degree at which this occurs is governed by the Poisson’s ratio.


Poisson's ratio formula
Note:
  • There is a –ve sign because εlat usually has an opposite sign to εlong, so the –ve sign makes the ratio +ve.
  • Very important property when we look at generalised Hooke’s law.

Shear modulus, G

Basically the same as Young’s modulus E, but for shear conditions:


Shear modulus formula
Note:
  • G measures the shear stiffness of the material. The higher the G, the less it “tilts” under the same shear loading.
  • Also usually very large in magnitude, and is normally prescribed in GPa.

Great! You've completed Chapter 1. Let’s look at C2: Axial Load now.

Young’s modulus, E

Young's modulus formula
Note:
  • E measures the stiffness of the material. The higher the E, the less it strains under the same stress.
  • E is usually constant for the same material (e.g. Esteel = 200 GPa), so if we know the σ we can find ε using E, and vice-versa
  • The magnitude of E is usually very large, and GPa (109) is commonly used.
  • In experiments, stress is usually obtained by measuring strain using strain rosettes, and then converted to stress via E.

Poisson’s ratio, ν

Poisson ratio deformation effect

Have you ever noticed that, when you stretch anything (say a rubber block), part of the material actually thins or necks? That’s because the material needs to be redistributed to allow it to stretch. The degree at which this occurs is governed by the Poisson’s ratio.


Poisson's ratio formula
Note:
  • There is a –ve sign because εlat usually has an opposite sign to εlong, so the –ve sign makes the ratio +ve.
  • Very important property when we look at generalised Hooke’s law.

Shear modulus, G

Basically the same as Young’s modulus E, but for shear conditions:


Shear modulus formula
Note:
  • G measures the shear stiffness of the material. The higher the G, the less it “tilts” under the same shear loading.
  • Also usually very large in magnitude, and is normally prescribed in GPa.

Great! You've completed Chapter 1. Let’s look at C2: Axial Load now.

engineering core courses

COURSES FEATURES THE STORY CONTACT US ECC facebook link
engineering core courses